Implementing Balanced Deletion for B+ Trees

mgcadmin 08-20-2025

When it comes to data structures - especially self balancing data structures - it is no secret that the algorithms for removing an entry are often many, many times more complex than the algorithms for adding a value. Anyone who's tried to wrap their noggin around balanced deletion in Red/Black tree knows exactly what I'm talking about.

The situation for B trees - the family of data structures which Red/Black trees abstract - isn't much different. While not as difficult to implement as "plain" B Trees despite sharing a common heritage, B+ trees present their own constraints for removing an element from the tree. 

A Unique Challenge

Traditional B Trees  are structured in a fashion similar to binarys earch trees in that data is stored in the same node as the key that references it. A B+ tree on the other hand is an indexing data structure: Keys and Values stored separately. With this reasoning in mind it may help to think about B+ Trees as if they were a combination of two different data structures instead of a single unified data structure. With this model, we imagine the upper portion of the tree to serve as an index to guide us to the correct node of a linked list which plays the role of the leaf level of the tree.

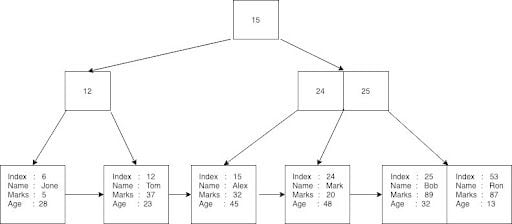
A B+ trees upper levels index into the linked list at the leaf level

We can think of removing a value from a B+ tree being performed in two steps. The first step is the actual removal of the referenced value from the linked list. Once that is accomplished, we then move to the second step of performing any rebuilding of the index which may have become invalid by removing the leaf value.

Removing an entry from the leaf level is easy enough, Once we find the correct leaf node, removing a value reduces to the case of deleting an entry from a sorted array:

template <class K, class V>
void BPNode<K,V>::eraseAt(int idx) {
        for (int j = idx; j < n-1; j++) {
            data[j] = data[j+1];
        }
        n--;
}

But what do we do about nodes that become completey empty upon removal of a key? And what do we do about the upper levels of the tree, specifically they keys which pointed us to the value? After all, being an indexed structure, other values may be depending on that value to drive a search to them, or the value that indexed to the item being erased is a related albeit different key. We can't orphan the other values in a node when we erase one value from it.

In todays post I'm going to cover the implementation of a deletion method for B+ trees by starting with the simplest naiive approach, and gradually adding functionality until we have a full deletion method which maintains both height and balance.

We will begin by simply allowing nodes to underflow, only removing keys from internal nodes when the nodes they point to become empty. Next, we will implement changes to propagate changes in keys to the index, but not perform any redistribution of keys amongst siblings should a node drop below M/2 keys. Finally, by implementing a merge method for underflowing nodes we will have an implementation which maintains both height and balance in our B+ tree.

I'm going to be building off the bottom up B+ tree code presented in my post on Memory Resident B+ Trees so if you haven't read that post, you might want to give it a read first to get up to speed. With that said, lets do it.

The Naiive Approach

Removing a value from the index starts at the root, and works towards the leaf where if the value exists it will be removed as was depicted in the previous section. Regardless of if the current node is a leaf or not, the first thing we do is check the node for the key we want to remove. 

If we are not at a leaf not, we first need to check if the result of the search for the key was successful. If the key we are searching for is not in the node, then we need to find the node with a the largest key still less than the key we are searching for. This is the purpose of the floor() method. 

void remove(BPNode<K,V>* node, K key) {
      int idx = node->find(key);
      if (node->isLeaf()) {
          if (idx != -1) {
             node->eraseAt(idx);
          }
      } else {
          idx = (idx == -1) ? node->floor(key):idx;
          remove(node->at(idx).next, key);
          if (node->at(idx).next->isEmpty()) {
              node->eraseAt(idx);
          }
      }
}

After traversing the tree to the leaf (and presumably removing a value from the leaf level) we check each node as the stack unwinds for the case where we may have erased the only entry in a node, which would leave an empty node with nothing pointing at it. In this case, we delete both the empty node and the key in the index which pointed to the empty node. This process cascades upward towards the root. In this way, the viability of the Index is preserved, despite letting nodes underflow as we erase values.

max@MaxGorenLaptop:~/btrees$ ./bpt
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a a a ] [ b e ] [ e e e ] [ l l l ] [ m m ] [ p r ] [ s t x ] 

Erase: a
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a a ] [ b e ] [ e e e ] [ l l l ] [ m m ] [ p r ] [ s t x ]   
--------------
Erase: s
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a a ] [ b e ] [ e e e ] [ l l l ] [ m m ] [ p r ] [ t x ]
--------------
Erase: m
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a a ] [ b e ] [ e e e ] [ l l l ] [ m ] [ p r ] [ t x ]
--------------
Erase: a
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ b e ] [ e e e ] [ l l l ] [ m ] [ p r ] [ t x ]
--------------
Erase: l
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ b e ] [ e e e ] [ l l ] [ m ] [ p r ] [ t x ]
--------------
Erase: l
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ b e ] [ e e e ] [ l ] [ m ] [ p r ] [ t x ]
--------------
Erase: b
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ e ] [ e e e ] [ l ] [ m ] [ p r ] [ t x ]
--------------
Erase: t
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ e ] [ e e e ] [ l ] [ m ] [ p r ] [ x ]
--------------
Erase: r
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ e ] [ e e e ] [ l ] [ m ] [ p ] [ x ]
--------------
Erase: e
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ e ] [ e e ] [ l ] [ m ] [ p ] [ x ]
--------------
Erase: e
[ a e m ]
[ a b ] [ e l ] [ m p s ]
[ a ] [ e ] [ e ] [ l ] [ m ] [ p ] [ x ]
--------------
Erase: e
[ a e m ]
[ a b ] [ l ] [ m p s ]
[ a ] [ e ] [ l ] [ m ] [ p ] [ x ]
--------------
Erase: x
[ a e m ]
[ a b ] [ l ] [ m p ]
[ a ] [ e ] [ l ] [ m ] [ p ]
--------------
Erase: a
[ a e m ]
[ b ] [ l ] [ m p ]
[ e ] [ l ] [ m ] [ p ]
--------------
Erase: m
[ a e m ]
[ b ] [ l ] [ p ]
[ e ] [ l ] [ p ]
--------------
Erase: p
[ a e ]
[ b ] [ l ]
[ e ] [ l ]
--------------
Erase: l
[ a ]
[ b ]
[ e ]
--------------
Erase: e

--------------

A funny side effect implementing delete in this way, as you can see, the tree's height does not shrink as we remove items. That wont really do, so how can we also handle the gradual reduction of height that accompanies removing items? We will return to this problem after first addressing the other issue: the index, while working properly, is less exact the more we remove items. Let's fix that by propagating changes to the index.

Erasing Values While Preserving the Integrity of the Index

Instead of just removing links to nodes when they become empty, we can also do a better job of maintaining the index by replacing the keys in the internal nodes when the value they direct to is removed from the tree.

link erase(link curr, K key, int ht) {
        if (ht == 0) {
            int j = curr->find(key);
            if (j != -1) {
                curr->eraseAt(j);
            }
        } else {
            int j = curr->floor(key);
            curr->page[j].next = erase(curr->page[j].next, key, ht-1);
            if (curr->page[j].next->n == 0) {
                curr->eraseAt(j);
            } else if (key == curr->page[j].info.key()) {
                curr->page[j] = entry(curr->page[j].next->page[0].info.key(), curr->page[j].next);
            }
        }
        return curr;
}

We can also manage the tree's height with a simple addition to the code. Just as a B tree can only grow from the root node, they also can only shrink in height from the root node. Should the root node come to posess a single key, we simply replace it by it's child, making that the new root node.

void erase(K key) {
       root = erase(root, key, height);
       if (root->n == 1) {
            link tmp = root;
            root = root->page[0].next;
            delete tmp;
            height--;
       }
}

Let's see how these changes stack up:

[ a i ] 
[ a e ] [ i n r ]
[ a c ] [ e g h ] [ i l m ] [ n p ] [ r s x ]
Erase: a
[ c i ]
[ c e ] [ i n r ]
[ c ] [ e g h ] [ i l m ] [ n p ] [ r s x ]

------------
Erase: s
[ c i ]
[ c e ] [ i n r ]
[ c ] [ e g h ] [ i l m ] [ n p ] [ r x ]

------------
Erase: e
[ c i ]
[ c g ] [ i n r ]
[ c ] [ g h ] [ i l m ] [ n p ] [ r x ]

------------
Erase: r
[ c i ]
[ c g ] [ i n x ]
[ c ] [ g h ] [ i l m ] [ n p ] [ x ]

------------
Erase: c
[ g i ]
[ g ] [ i n x ]
[ g h ] [ i l m ] [ n p ] [ x ]

------------
Erase: h
[ g i ]
[ g ] [ i n x ]
[ g ] [ i l m ] [ n p ] [ x ]

------------
Erase: i
[ g l ]
[ g ] [ l n x ]
[ g ] [ l m ] [ n p ] [ x ]

------------
Erase: n
[ g l ]
[ g ] [ l p x ]
[ g ] [ l m ] [ p ] [ x ]

------------
Erase: g
[ l p x ]
[ l m ] [ p ] [ x ]

------------
Erase: x
[ l p ]
[ l m ] [ p ]

------------
Erase: m
[ l p ]
[ l ] [ p ]

------------
Erase: p
[ l ]

------------
Erase: l
[ ]
------------

Much better. But We can still do more. Notice how we end up with alot of nodes with a single entry, cant we just stick that in its neighbor or something? Turns out: yes, we certainly can. This simple idea leads us to our final implementation, which takes that idea and expands on it: instead of waiting for a node to drop to a single key before taking action, why not pre-emptively merge a node with its neighbor should the sum of their entries not cause the node to overflow? Sounds like we're going to need a merge procedure.

Merging Siblings Nodes

The procedure to merge two nodes is simple, but it has some constraints which are not immediately obvious. The merge routine takes two nodes as its parameters, a and b. These nodes are expected to be logical neighbors: if node 'a' is page[j].child, then node b should be page[j+1].child (or j-1 & j, respectively). This condition must hold. Additionally, neither node should have more than M/2 keys. 

link merge(link a, link b) {
        for (int i = 0; i < b->n; i++)
            a->page[a->n++] = b->page[i];
        b->n = 0;
        a->next = b->next;
        if (b->next != nullptr) {
            b->next->prev = a;
        }
        delete b;
        return a;
}

With our merge procedure we now have everything needed to implement the full balanced B+ Tree deletion algorithm, so without further ado, lets check out the full implementation.

Balanced B+ Tree Deletion

Upon entering the current node, we check to see if the key being searched for is present. Depending on whether or not the current node is a leaf node one of two things will happen. If we are at a leaf node and the key being searched for is present, we delete the entry at that index in the leaf node.

If we're not at a leaf node, we use the floor() method to find the proper link to continue the search with, and proceed down the tree. As the stack unwinds, we once again check if we are at leaf node, and if so, simply return it. If were currently visiting an internal node however, we call the balance routine on the current node.

link erase(link curr, K key, int ht) {
       int j = curr->find(key);
       if (ht == 0 && j != -1) {
           curr->eraseAt(j);
       } else {
            j = curr->floor(key);
           curr->page[j].child = erase(curr->page[j].child, key, ht-1);
       }
       return ht == 0 ? curr:rebalance(curr, key, j);
}


link rebalance(link curr, K key, int j) {
        if (curr->page[j].child->n < M/2) {
            if (j+1 < curr->n && (curr->page[j].child->n + curr->page[j+1].child->n <= M)) {
               curr->page[j].child = merge(curr->page[j].child, curr->page[j+1].child);
               curr->eraseAt(j+1);
           } else if (j-1 >= 0 && (curr->page[j].child->n + curr->page[j-1].child->n <= M)) {
                curr->page[j-1].child = merge(curr->page[j-1].child, curr->page[j].child);
                curr->eraseAt(j);
           }
        } 
        if (key == curr->page[j].info.key()) {
            curr->page[j] = entry(curr->page[j].child->page[0].info.key(), curr->page[j].child);
        }
        return curr;
}

The balance routine works by checking if the node we (potentially) just removed an entry from to see if the number of entries it holds has dropped below the balance threshold of M/2. In the event the node underflows we check if there is a node to the left or right we could merge with, and if found merge them while removing the merged nodes key from it's parent node.

void erase(K key) {
       root = erase(root, key, height);
       if (root->n == 1 && height > 0) {
            root = chopRootAndShrink(root);
       }
}


link chopRootAndShrink(link old_root) {
        link tmp = root;
        root = root->page[0].child;
        delete tmp;
        height--;
        return root;
}

Shrinking from the root still proceeds the same way, reducing the height of the tree when the root node drops to a single entry. With these changes made, lets run our example one more time:

Starting Tree:
[ a i ]
[ a e ] [ i n r ]
[ a c ] [ e g h ] [ i l m ] [ n p ] [ r s x ]

Erase: a
[ c i n r ]
[ c e g h ] [ i l m ] [ n p ] [ r s x ]

Erase: s
[ c i n r ]
[ c e g h ] [ i l m ] [ n p ] [ r x ]

Erase: e
[ c i n r ]
[ c g h ] [ i l m ] [ n p ] [ r x ]

Erase: r
[ c i n ]
[ c g h ] [ i l m ] [ n p x ]

Erase: c
[ g i n ]
[ g h ] [ i l m ] [ n p x ]

Erase: h
[ g n ]
[ g i l m ] [ n p x ]

Erase: i
[ g n ]
[ g l m ] [ n p x ]

Erase: n
[ g p ]
[ g l m ] [ p x ]

Erase: g
[ l p ]
[ l m ] [ p x ]

Erase: x
[ l m p ]

Erase: m
[ l p ]

Erase: p
[ l ]

Erase: l
[ ]

Perfect,

That's all I've got for today, until next time Happy Hacking!

Further Reading

[1] Sedgewick, R. "Algorithms in C++" 3rd ed.

[2] Sithart & Tarjan, "Deletion Without Rebalancing in Multiway Search Trees", https://sidsen.azurewebsites.net/papers/relaxed-b-tree-tods.pdf

[3] Shaffer "Data Structure & Algorithm Analysis in Java", https://people.cs.vt.edu/shaffer/Book/

[4] My full B+ tree implementation https://github.com/maxgoren/BPlusTree

---