Improving the Space Efficiency of Suffix Arrays

mgcadmin 09-28-2025

Suffix Arrays are a neat data structure, to say the least. They allow us to perform efficient substring searchs, "keyword in context" searches, in addition to enabling us to compute the longest common prefix of a string in linear time. Suffix arrays are themselves a space efficient (comparatively, at least) take on another data structure: the suffix trie.

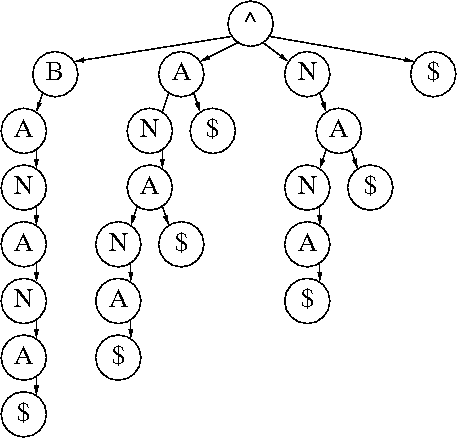
A Suffix Trie

Suffix Tries are constructed from inserting every possible suffix of an input string into a Prefix-Trie. Depending on how they are encoded, suffix tries can require an enormous amount of space. The suffix array was developed to address this issue by preserving the functionality of a suffix trie while forgoing the actual construction of one.  This is accomplished by leveraging the power of sorting & binary search over a table of suffixes. 

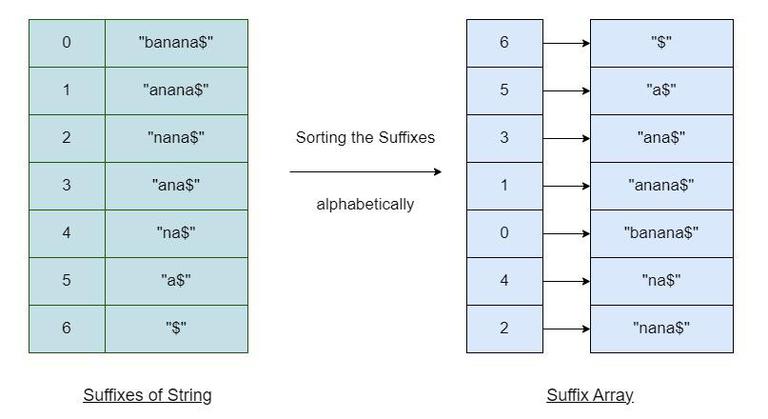
Suffix Array Construction

While requiring far less space than a trie, this table of suffixes still requires a not-insginificant amount of space. The question then becomes, do we actually need the suffix table? As it would turn out, so long as we have the input string, than we do not actually need the suffix table either. Let's see how.

A closer look at the problem

Many resources, textbooks included[1], when discussing the implementation of a suffix array utilize the construction of an explicit suffix table, usually along the lines of something like this:

struct Suffix {
        string suffix;
        int index;
        Suffix(string s = "", int idx = 0) : suffix(s), index(idx) { }
};

int N = input.length();
vector<Suffix> suffTable;
for (int i = 0; i < N; i++) {
     suffTable.push_back(Suffix(input.substr(i, N-i), i));
}
sort(suffTable.begin(), suffTable.end(), [](const Suffix& a, const Suffix& b) { return a.suffix < b.suffix; });

While the above code is technically correct and has the benefit of being very easy to understand it is also an exceedingly inefficient way of implementing a suffix array. Additionally, it is also impractical for larger strings due to the amount of space needed to store all of those suffixes. The space complexity of the above implementation is actually O(N^2). It's still not as bad as a suffix trie, but it's definitely not great either. 

Suffix Arrays Without the Suffix Table

If we want the suffix array to scale to larger pieces of text we will need to do something to reduce that cubic space complexity, and we can do just that by exploiting some properties of the suffixes themselves. The only unique piece of information and coincidentally the only part of the suffix array we need to save, is the index portion of Suffix  data structure. The rest of the data is just duplicating information we already have in the form of the input text.

In the explicit suffix table version we sorted the vector by doing a string comparison on the suffixes. We can do the samething using the index field and a little bit of indirection. C++ allow us to pass an objects 'this' context to be captured by a lambda, denoted by the prescence of the '[&]' symbol in the lambda definition below.

This is important because it means we can access variables from the lexical context of the class its defined in. By now, I'm sure you can see where I'm going with this, so i'll let the code speak for it's self.

class SuffixArray {
    private:
        string input;
        vector<int> suffArr;
        int N;
    public:
        SuffixArray(string str) {
            input = str;
            N = str.length();
            suffArr.resize(N);
            iota(suffArr.begin(), suffArr.end(), 0); //fill suffArr with 0 .. N
            sort(suffArr.begin(), suffArr.end(), [&](int a, int b) { return input.substr(a) < input.substr(b); });
        }
        bool search(string pattern) {
            int l = 0, r = N-1;
            while (l <= r) {
                int m = (l+r)/2;
                string toComp = input.substr(suffArr[m], pattern.length());
                if (pattern < toComp) r = m - 1;
                else if (pattern > toComp) l = m + 1;
                else return true;
            }
            return false;
        }
};

Just like that, we've managed to reduce the space complexity of our suffix array from O(N^2) down to O(N) from making use of a simple observation regarding the structure of the data it's self. Not too shabby. Until next time, Happy Hacking!

Further Reading

[1] Sedgewick, R. "Algorithms" 4th ed. ch. 5 

---