re   ->  (re)#

The octothorpe serves as a defacto "accept" state tacked on to the end of the regular expression string.

char* augmentRE(char* orig) {
    char* fixed = malloc(sizeof(char)*strlen(orig)+3);
    sprintf(fixed, "(%s)#", orig);
    return fixed;
}

Once we have augmented the regular expression using the procedure shown above we can move on to generating an AST for our regular expression string.

From an RE to an AST

Each node is assigned a unique number, which represents both is place in the ast AND its position in the regular expression string. Every node also contains pointers to the firstpos, lastpos, and followpos sets for the position the node represents, as well as the token for that position. 

typedef struct re_ast_ {
    int type;
    int number;
    Token token;
    Set* firstpos;
    Set* lastpos;
    Set* followpos;
    struct re_ast_* left;
    struct re_ast_* right;
} re_ast;

There are many ways to build an AST from a regular expression string. The simplest way is to convert the expression to it's postfix form and then construct the tree bottom up using a stack. I have covered how to convert regular expressions from infix to postfix using the shunting yard algorithm in my post on Thompson's Construction, and so will not repeat it here. I will instead proceed with the assumption that your regular expression string has already been converted to postfix.

re_ast* makeTree(Token* tokens) {
    int len = tokensLength(tokens);
    re_ast* st[len];
    int sp = 0;
    for (Token* it = tokens; it != NULL; it = it->next) {
            if (isOp(*it)) {
                re_ast* n = makeNode(1, *it);
                switch (it->symbol) {
                    case RE_OR:
                    case RE_CONCAT:
                        if (sp < 2) {
                            printf("Error: stack underflow for binary operator %c\n", it->symbol);
                            exit(EXIT_FAILURE);
                        }
                        n->right = (sp > 0) ? st[--sp]:NULL;
                        n->left = (sp > 0) ? st[--sp]:NULL;
                        break;
                    case RE_STAR: 
                        n->left = (sp > 0) ? st[--sp]:NULL;
                        break;
                    case RE_QUESTION: {
                        free(n);
                        n = makeNode(1, *makeToken(RE_OR, '|'));
                        n->left = (sp > 0) ? st[--sp]:NULL;
                        n->right = makeNode(2, *makeToken(RE_EPSILON, '&'));
                    } break;
                    case RE_PLUS: {
                        free(n);
                        n = makeNode(1, *makeToken(RE_CONCAT, '@'));
                        re_ast* operand = (sp > 0) ? st[--sp]:NULL;
                        n->left = operand;
                        n->right = makeNode(1, *makeToken(RE_STAR, '*'));
                        n->right->left = cloneTree(operand);
                    } break;
                    default: break;
                }
                st[sp++] = n;
            } else {
                re_ast* t = makeNode(2, *it);
                st[sp++] = t;
            }
    }
    return st[--sp];
}

Notice that for operators '+' and '?' that unlike for thompsons construction we do not create nodes for those operators directly, we instead build tree's for their equivelant regular expressions using concat, or, and kleene star. The reason for this will be explained in more detail below, but suffice it to stay, a little tree-rewriting now saves alot of implementation hassle later.

re_ast* cloneTree(re_ast* node) {
    if (node == NULL)
        return NULL;
    re_ast* t = makeNode(node->type, node->token);
    t->type = node->type;
    t->token = node->token;
    t->left = cloneTree(node->left);
    t->right = cloneTree(node->right);
    return t;
}

The ast is built before the sets are created, so we dont have copy them during the clone operation.

Numbering the Nodes

Assigning numbers to the nodes is a 2-pass process accomplished via a depth first search. The first pass assigns numbers to the leaf nodes, with the second pass assigning numbers to the internal nodes. We also place each node in the node position table immediately after we assign it's number: the number is used to index into in the table.

re_ast** ast_node_table;

int isLeaf(re_ast* node) {
    return (node->left == NULL && node->right == NULL);
}

int numleaves = 0;
int nonleaves = 0;

void number_nodes(re_ast* node, int pass) {
    if (node != NULL) {
        number_nodes(node->left, pass);
        number_nodes(node->right, pass);
        if (isLeaf(node)) {
            if (pass == 1) {
                node->number = ++numleaves;
                ast_node_table[node->number] = node;
            }
        } else {
            if (pass == 2) {
                node->number = ++nonleaves;
                ast_node_table[node->number] = node;
            }
        }
    }
}

After assigning numbers to each node, our AST will look something like the following:

AST:
  <CONCAT, @> {12}
    <CONCAT, @> {11}
      <CONCAT, @> {10}
        <CONCAT, @> {9}
          <STAR, *> {8}
            <OR, |> {7}
              <CHAR, a> {1}
              <CHAR, b> {2}
          <CHAR, a> {3}
        <CHAR, b> {4}
      <CHAR, b> {5}
    <CHAR, #> {6}

Having built our AST and populated the position table, we can start initialized our firstpos, lastpos, and followpos sets.

void initAttributeSets(int size) {
    for (int i = 0; i < size+1; i++) {
        if (ast_node_table[i] != NULL) {
            ast_node_table[i]->firstpos = createSet(size+1);
            ast_node_table[i]->lastpos = createSet(size+1);
            ast_node_table[i]->followpos = createSet(size+1);
        }
    }
}

Nullable, Firstpos, Lastpos, and Followpos

Using the table below, we derive the rules of populating the sets for each position(n) in our RE. The firstpos and lastpos sets are constructed by performing depth first traversals over the AST, using the results of nullable(n), to populate the firstpos set, and then the lastpos set. 

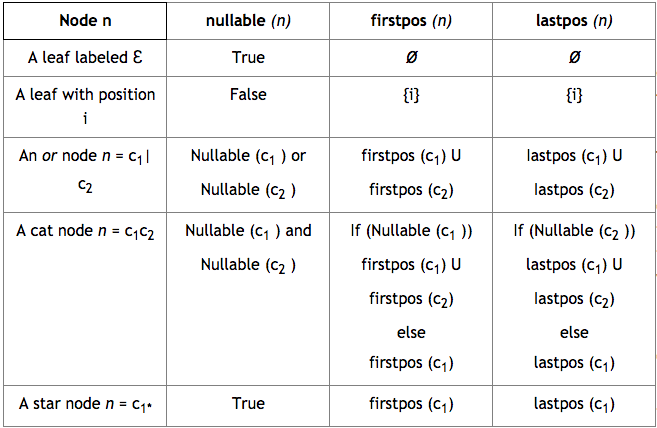
 Once those set's have been constructed, we can create the Followpos table. Interestingly, the followpos table is itself an NFA, albeit one lacking epsilon transitions - it is actually the same automaton you would create from Glushkovs Construction!

Nullable

Unlike firstpos, lastpos, and followpos which are implemented as sets, nullable is implemented as a function since nullable(n) is a single immutable value. It is also possible to compute and cache nullable(n) as the node n is being created, storing nullable(n) as a property of n.

bool nullable(re_ast* node) {
    if (node == NULL)
        return false;
    if (isLeaf(node) && node->token.symbol == RE_EPSILON)
        return true;
    if (isLeaf(node) && (node->token.symbol == RE_CHAR || node->token.symbol == RE_PERIOD))
        return false;
    if (node->token.symbol == RE_OR)
        return nullable(node->left) || nullable(node->right);
    if (node->token.symbol == RE_CONCAT) {
        return nullable(node->left) && nullable(node->right);
    }
    if (node->token.symbol == RE_STAR)
        return true;
    return false;
}

Firstpos and Lastpos

void calcFirstandLastPos(re_ast* node) {
    if (node != NULL) {
        calcFirstandLastPos(node->left);
        calcFirstandLastPos(node->right);
        if (isLeaf(node)) {
            setAdd(node->firstpos, node->number);
            setAdd(node->lastpos, node->number);
        } else if (node->token.symbol == RE_OR) {
            mergeFirstPos(node);
            mergeLastPos(node);
        } else if (node->token.symbol == RE_CONCAT) {
            if (nullable(node->left)) {
                mergeFirstPos(node);
            } else if (node->left) {
                node->firstpos = setUnion(node->firstpos, node->left->firstpos);
            }
            if (nullable(node->right)) {
                mergeLastPos(node);
            } else if (node->right) {
                node->lastpos = setUnion(node->lastpos, node->right->lastpos);
            }
        } else if (node->token.symbol == RE_STAR && node->left) {
            node->firstpos = setUnion(node->firstpos, node->left->firstpos);
            node->lastpos = setUnion(node->lastpos, node->left->lastpos);
        }
    }
}

calcFirstAndLastPos() perform a post-order depth first traversal of the AST inorder to build the sets. Post order traversal is used because nodes higher in the tree contain sets derived from nodes  lower in the tree and so post order traversal assures those sets have already been constructed first. 

void mergeFirstPos(re_ast* node) {
    if (node->left) {
        node->firstpos = setUnion(node->firstpos, node->left->firstpos);
    }
    if (node->right) {
        node->firstpos = setUnion(node->firstpos, node->right->firstpos);
    }
}

void mergeLastPos(re_ast* node) {
    if (node->left) {
        node->lastpos = setUnion(node->lastpos, node->left->lastpos);
    }
    if (node->right) {
        node->lastpos = setUnion(node->lastpos, node->right->lastpos);
    }
}

The helper methods mergeFirstPos() and mergeLastPos() are used to assign to a node n the result of performing a set union on a given nodes left and right child's sets with its own.

Followpos

The purpose of the initial node numbering and computing of the firstpos/lastpost sets were in service of generating the followpos table. As such, we wrap the interface to all of them into a single procedure, computeFollowPos() which takes our AST as input, and output's the numbered AST and Followpos table.

void computeFollowPos(re_ast* node) {
    ast_node_table = malloc(sizeof(re_ast*)*(748));
    numleaves = 0;
    number_nodes(node, 1);
    nonleaves = numleaves;
    number_nodes(node, 2);
    initAttributeSets(nonleaves+1);
    calcFirstandLastPos(node);
    calcFollowPos(node);
}

Just as was done for firstpos and lastpos, followpos is constructed by performing a post-order depth first traversal of the regular expressions AST.

void calcFollowPos(re_ast* node) {
    if (node == NULL)
        return;
    if (node->token.symbol == RE_CONCAT) {
        if (!node->left || !node->right) {
            printf("ERROR: RE_CONCAT node %d missing children (left=%p, right=%p)\n",
                   node->number, (void*)node->left, (void*)node->right);
            return;
        }
    }
    calcFollowPos(node->left);
    calcFollowPos(node->right);
    if (node->token.symbol == RE_CONCAT) {
        if (node->left == NULL || node->right == NULL)
            return;
        for (int i = 0; i < node->left->lastpos->n; i++) {
            int t = node->left->lastpos->members[i];
            ast_node_table[t]->followpos = setUnion(ast_node_table[t]->followpos, node->right->firstpos);
        }
    }
    if (node->token.symbol == RE_STAR) {
        for (int i = 0; i < node->lastpos->n; i++) {
            int t = node->lastpos->members[i];
            ast_node_table[t]->followpos = setUnion(ast_node_table[t]->followpos, node->firstpos);
        }
    }
}

Constructing A DFA from Followpos Sets

We've covered _alot_ of material: we've constructed an AST from the regular expression, annotated our augmented regular expression with positional information for each node, and then used those positional sets to construct the followpos table. It is this followpos table from which we will construct the actual DFA for the regular expression, so stick around for part 2 where I show you how to make the final leap from a regular expression to a DFA. Until then, Happy Hacking!

Further Reading

[1] Aho, Sethi, Ullman, "Compilers Principles, Techniques, And Tools", 1986