Branching out: The Trie

mgcadmin 06-05-2023

Along with arrays and lists, trees are the one of the most fundamental data structures in computer science, if not THE fundamental structure. There are many, many different tree-based data structures tailored to all sorts of use cases.

In the past I've covered many different kinds of binary trees, including self-balancing binary search trees, and binary heaps. So I thought I would *sunglasses on* branch out, and explore trie data structures.

What is a Trie anyway?

A trie is a tree structure purposely suited for storing and retrieving text strings. It is often used in auto complete and spell checking, as well as IP address routing algorithms. As far as how to pronounce trie, the jury is still out. It's name derives from the word re-trie-val, and thus should be pronounced "tree", though many people pronounce it "try" so as to distinguish them from other kinds of trees, and i personally follow this.

Tries come in many variants as well: radix tires, digital tries, binary tries, compressed tries, and PATRICIA tries just to name a few. What they all share in common is that it is the digital properties of the keys rather than the keys themselves that determine the branching pattern of nodes. In this post I will be covering prefix tries, sometimes referred to as "Suffix Tree's" as they have a use case similar to the previously covered suffix arrays.

Implementing a Trie

Unlike in a binary search tree, where inserting the strings "dog" and "cat" would directly compare "dog" to "cat" to determine that whether we should insert the "cat" node as the left or right child of the "dog" node, in a trie each individual letter gets a node: 'd' branches to 'o' branches to 'g', etc.

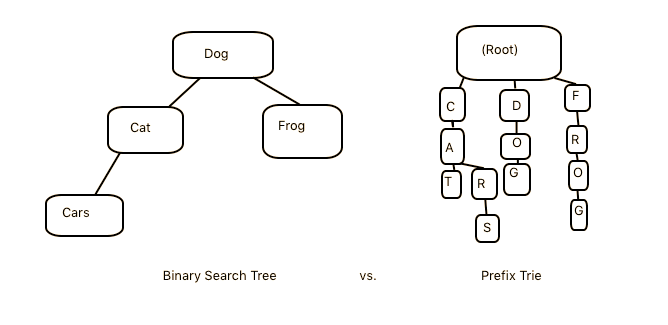
As you can see, the structure of a Trie's Node will differ significantly from a binary search tree, as does the insertion process itsself.

const int RADIX = 256;

struct node {
     char c;
     bool endOfKey;
     node** next;
     node(char _c = 'a', bool eok = false) {
         c = _c; endOfKey = eok;
         next = new node*[RADIX];
     }
     ~node() {
          for (int i = 0; i < RADIX; i++)
             if (next[i] != nullptr)
                delete next[i];
          delete [] next;
     }
};

The node structure highlights one of the downsides of tries: they tend to waste a lot of space. We need to have a child position for all characters we wish to be able to represent in the tree. One could be more space efficient by using a function to map the characters to a number other than ASCII integer representation, but for the sake of simplicity, i just make the child array large enough to hold any printable character without needing additional processing.

Another approach to making a trie more memory efficient that many people use is to have a hash table instead of an array for pointing to the children:

struct node {
     char c;
     bool endOfKey;
     unordered_map<char, node*> next;
};

While this does make better use of memory, we lose one of the very useful properties of tries: when using an array for the child pointers, a pre-order traversal of the trie will yield the stored strings in alphabetical order. This is not possible when using a hash table as hash tables by their nature are unordered collections.

The root node of a Trie is a special case: It does not represent a value itself, its just there as a place for the branching to begin, thus an "empty" trie is not a null root node, it is a root node with no children.

To insert a string into a trie, we start at the root, and go character by character through the key string, checking if the current node has a child node for that letter, and if it doesn't we insert a node for that character, otherwise we simply traverse to the child node and continue this "check and insert-or-continue" until we run out of characters in the key and mark the last node as "end of key".

void insert(string key) {
    node* x = root;
    for (char c : key) {
         if (x->next[c] == nullptr) {
             x->next[c] = new node(c, false);
         }
         x = x->next[c];
    }
    x->endOfKey = true;
    N++;
}

As you can see, the insertion process translates to a very straightforward iterative algorithm. Searching for a key works much the same way:

bool contains(string key) {
       node* x = root;
       int i = 0;
       for (i = 0; i < key.size() && x->next[key[i]] != nullptr; i++) { 
                x = x->next[key[i]]; 
       }
       if (i == key.size() && x->endOfKey)
             return true;

       return false;
 }

Once again we walk the tree as we walk the string, if when we exit the loop, we have consumed the whole string and hit an end of key flag, then that key is in the trie. It would be trivial to also associate a value to the string and return that when we encounter the end of the key, thus transform our trie into a dictionary, or "trie map".

As mentioned earlier, a Trie will yield the keys it is storing in sorted order if you traverse it in preorder depth first fashion:

void preorder(node* h) {
    if (h != nullptr) {
        cout<<h->c<<" ";
        if (h->endOfKey) cout<<endl;
        for (int i = 0; i < RADIX; i++) {
            if (h->next[i] != nullptr) {
                preorder(h->next[i]);
            }
        }
    }
}

Putting It All Together

Now that you have a good idea of how a trie works, theres only one thing left to do: put it all together and take it for a test drive.

#include <iostream>
using namespace std;

#define RADIX 256

class Trie {
    private:
        struct node {
            char c;
            bool endOfKey;
            node** next;
            node(char _c = 'a', bool eok = false) {
                c = _c; endOfKey = eok;
                next = new node*[RADIX];
            }
        };
        node* root;
        int N;
        void preorder(node* h) {
            if (h != nullptr) {
                for (int i = 0; i < RADIX; i++) {
                    if (h->next[i] != nullptr) {
                        cout<<h->next[i]->c;
                        preorder(h->next[i]);
                        if (h->next[i]->endOfKey) { 
                            cout<<"\n";
                        }
                    }
                }
            }
        }
    public:
        Trie() {
            root = new node('*', false);
            N = 0;
        }
        int size() { return N; }
        bool empty() { return size() == 0; }
        void insert(string key) {
            node* x = root;
            for (char c : key) {
                if (x->next[c] == nullptr) {
                    x->next[c] = new node(c, false);
                }
                x = x->next[c];
            }
            x->endOfKey = true;
            N++;
        }
        bool contains(string key) {
            node* x = root;
            int i = 0;
            for (i = 0; i < key.size() && x->next[key[i]] != nullptr; i++) { 
                x = x->next[key[i]]; 
            }
            if (i == key.size() && x->endOfKey)
                return true;
            return false;
        }
        void preorder() {
            preorder(root);
            cout<<endl;
        }
};

int main() {
    string strs[] = { "cat", "dog", "cars", "frog", "frizbee", "horse", "home", "hate"};
    Trie trie;
    for (string s : strs) {
        trie.insert(s);
    }
    trie.preorder();
    return 0;
}

[maxs-MacBook-Pro:~]% gcc trieset.c -o trieset && ./trieset 
 cars
   t
 dog
 frizbee
   og
 hate
  ome
   rse
 [maxs-MacBook-Pro:~]% 

 

---