Lossless Compression Part II: The LZ77 Algorithm
The Lempel-Ziv family of algorithms were introduced by Abraham Lempel and Jacob Ziv in two papers over the course of 1977 & 1978. The algorithms detailed in those papers have come to be known as lz77 (lz1) and lz78(lz2), respectively. Since being introduced, their adoption has been practically universal - particularly lz77 and it's many variants.
The Lempel-Ziv algorithms are dictionary based encoding methods suitable for lossless compression. They are can be described as generalizations of run length encoding, a simpler but less adabtable method of lossless compression. Instead of character and count pairs as generated by canonical run length encoding, the Ziv Lempel algorithms replace strings of repeated text with "back references" to their earlier appearance in the text.
In todays post I'm going to cover implementing the lz77 algorithm, and using it to compress and decompress files. This post relies on the BitStream class covered in my previous post on the topic, so give that a read if you haven't done so. With that said, let's get to it.
The lz77 Algorithm
The algorithm introduced by Ziv and Lempel in their 1977 paper has gone on to be one of, if not THE most used compression algorithms of all times. Lz77 has spawned countless variants, such as LZSS, LZMA, and LZH just to name a few. It is also one of the major components of the DEFLATE algorithm.
The Algorithm works by maintaining two buffers: the "search" buffer, and the "lookahead" buffer. Both of these buffers are pointers into the text being encoded, and are calculated relative to the current position in the text. Taken together, they are referred to as the "sliding window". The search buffer is a portion of text that has already been encoded - but in its unenoded form. The sliding window as a whole generally ranges from 4Kb to 30kb in size. The lookahead buffer is a pre-determined amount of text ahead of the current position to be encoded, generally 256bytes.
These two buffers are compared to find the longest possible match of the text to be encoded, among the text that has already been encoded. In this way we can replace the repeated text with a back reference to it's already encoded self. The text to be encoded takes on an intermediate representation as a list of 'lz triples'.
LZ Triples, Offsets, and Buffer lengths
LZ triples are a simple data structure containing a tuple of values for the offset, length, and symbol that make up the "back references" into the text. The offset is the distance from the current position being encoded to the start of its previous place in the text - or 0 if it has not been seen yet. Length is the length of the match being encoded - again, possibly 0 if there is no previous occurence. The character is the next character after the match, in the lookahead buffer.
struct LZTriple {
int offset;
int length;
char symbol;
LZTriple(int o = 0, int l = 0, char c = '\0') : offset(o), length(l), symbol(c) { }
};
void print(LZTriple lzt) {
cout<<"("<<lzt.offset<<","<<lzt.length<<","<<lzt.symbol<<") ";
}
const int window_size = 4096;
const int lookahead_size = 256;The window_size and lookahead_size constants are the size of their respective buffers. These values are tunable, though changing their values can have a dramatic impact on the amount of compression, with a larger window_size allowing for farther references. However, you must be careful not to make it too large, as the longer the distance of the back reference, the more bits required to encode the offset.
Encoding Text with Lz77: Text In, LZ Triples Out
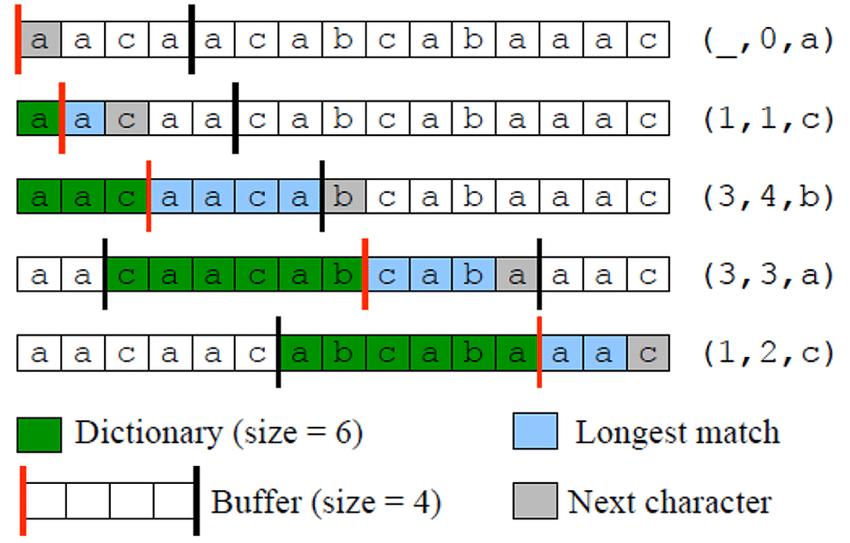
To convert our input text to a collection of LZ Triples, we iterate over the text while updating the bounds of the sliding window and lookahead buffer at each step. The search buffer is searched to find the longest match for the string beginning at the current position and extending in to the look ahead buffer.
vector<LZTriple> parseToTriples(string input) {
vector<LZTriple> results;
int curr_pos = 0;
while (curr_pos < input.size()) {
auto [match_len, match_left] = findLongestMatch(input, curr_pos);
LZTriple triple = makeTriple(input, curr_pos, match_len, match_left);
results.push_back(triple);
}
return results;
}Finding the longest match can be done by any of the well known pattern matching algorithms, such as the knuth-morris-pratt algorithm or the boyer-moore string searching algorithm. The Rabin-Karp hash finger print algorithm is particularly well suited for this task. I used a simple brute force search for the sake of brevity, but it should be noted that you can play with the actual matching algorithm used to determine which one suits your needs best.
int matchLength(string input, int window_pos, int lookahead_pos) {
int wp = window_pos, lp = lookahead_pos;
while (lp - lookahead_pos < lookahead_size && input[wp++] == input[lp++]);
return wp-1 - window_pos;
}
pair<int,int> findLongestMatch(string input, int& curr_pos) {
int match_len = 0, match_left = 0;
for (int win_start = max(0, curr_pos-window_size); win_start < curr_pos; win_start++) {
if (input[win_start] == input[curr_pos]) {
int ml = matchLength(input, win_start, curr_pos);
if (ml > match_len) {
match_len = ml;
match_left = win_start;
}
}
}
return make_pair(match_len, match_left);
}Different window size and lookahead length's will produce different sets of triples for the same file. For entries where no match is found, the offset and length are both 0, with the symbol being the current positions character. When a match is found, the offset is calculated by subtracting the matches starting position from the current position, and the symbol is the character in the lookahead buffer after the last character of the match.
LZTriple makeTriple(string input, int& i, int match_len, int match_left) {
LZTriple t;
if (match_len > 0) {
t.offset = i-match_left;
t.length = match_len;
t.symbol = input[i+match_len];
i += match_len+1;
} else {
t.offset = 0;
t.length = 0;
t.symbol = input[i];
i++;
}
return t;
}Once we have have our triples we are ready to encode our message as a string of bits, for which we will use the BitStream class developed in the previous post.
From Triples to Bits
Converting our triples to a format suitable for writing to a file is very easy thanks to the writeInt() and writeChar() methods we implemented in our BitStream class. We simply need to iterate over our vector of triples and directly write them to the BitStream. But! Before we do that, you may recall that we implemented a variable width write method for integers, and it is now that we can exploit some of our known properties of our data to garner further savings in space.
BitStream encodeFromTriples(vector<LZTriple>& triples) {
BitStream bits;
for (LZTriple t : triples) {
bits.writeInt(t.offset, 12);
bits.writeInt(t.length, 8);
bits.writeChar(t.symbol);
}
return bits;
}Remember when I said the length of the window size effects the number of bits used to encode it? By using a window_size of 4096 (4kb) we know that the distance of the offset will never need more than 12 bits of data to store. Likewise with the length, since the longest one of our matches can be is 256, we only need 8 bits to encode that number. For those keeping score, we have reduced the amount of bits required to store our triple from 40 bits down to 28 bits.
Once we have our data stored in the BitStream, we then write it to our output file byte wise resulting in our compressed file.
void BitStream::writeStreamToFile(string filename) {
std::ofstream file(filename+".mgz", std::ios::out|std::ios::binary);
start();
for (int j = 0; j < size(); ) {
int i = 0;
unsigned char byte = 0;
while (j < size() && i < 8) {
if (readBit()) {
byte |= (1 <<(7-i));
}
i++;
j++;
}
cout<<j<<": "<<byte<<endl;
file.write(reinterpret_cast<const char*>(&byte), sizeof(byte));
}
file.close();
}
void compressFile(string filename) {
StringBuffer sb;
sb.readBinaryFile(filename);
BitStream bits = encodeFromTriples(parseToTriples(sb.getBuffer()));
bits.writeStreamToFile(filename+".zz");
}Having compressed the data, our job is only have done. The data wouldn't be much good to use compressed if we then had no way of retrieving it! As such, we now turn our attention to decoding with lz77.
Uncompressing Files with lz77
Decoding a file that has been previously compressed with lz77 is very simple. It is pretty much the reverse of the steps we just did: Read the file, convert the file to a bit stream, decode the bit stream in to triples and then expand the text from the triples to yield the original uncompressed text.
void uncompressFile(string filename) {
StringBuffer sb;
sb.readBinaryFile(filename);
BitStream bs = stringBufferToBitStream(sb);
vector<LZTriple> triples = decodeToTriples(bs);
fstream outfile(filename+".out", ios::out|ios::binary);
if (outfile.is_open()) {
for (char c : expandFromTriples(triples))
outfile<<c;
outfile.close();
}
}
When converting the string buffer to a bit stream, we are treating them as even 8 bit bytes. We don't have to worry about the variable width integers until we do the actual decoding - for now, the bits are just bits.
BitStream stringBufferToBitStream(StringBuffer sb) {
BitStream bs;
while (!sb.done()) {
bs.writeChar(sb.get(), 8);
sb.advance();
}
return bs;
}Once we have our data as lz77 encoded bits we can decode them back into LZTriples. This is done by iterating over the bitstream and reading first our 12 bit offset, then our 8 bit length, and finally our 8 bit character. This step can can actually be combined with the previous step, but i separated them for clarity.
vector<LZTriple> decodeToTriples(BitStream bits) {
vector<LZTriple> triplets;
bits.start();
while (!bits.done()) {
LZTriple t;
t.offset = bits.readInt(12);
t.length = bits.readInt(8);
t.symbol = bits.readChar();
triplets.push_back(t);
}
return triplets;
}
Expanding LZ Triples back into text is, in short, a very satisfying thing to behold. And once you understand how it works you cant help but admire the cleverness of it. Whenever we encounter a length of zero, we simply add the symbol to the output. Otherwise, we first navigate to the point the previously expanded output and copy the length amount of characters to the ouput. That's it!
string expandFromTriples(vector<LZTriple> lz) {
string output;
for (LZTriple t : lz) {
if (t.length == 0) {
output.push_back(t.symbol);
} else if (t.offset == 1) {
for (int i = 0; i < t.length; i++)
output += output.substr(output.size()-1, 1);
output.push_back(t.symbol);
} else {
output += output.substr(output.size()-t.offset, t.length);
output.push_back(t.symbol);
}
}
return output;
}Now, when I said it was satisfying to watch, almost any real file will be far to large to appreciate the decoding in a stepwise fashion. But that doesn't stop us from observing the effect on some short strings, heck we have the algorithm at our disposal dont we? A few print statements at the bottom of the loop ought to do the trick. After compressing the string "AABABCAABBAC" down to triples, we can then pass it to our expandFromTriples() method, and having added print statements to the bottom of every loop, we are treated to the following output:
Expanding: (0,0,A) - A
Expanding: (1,1,B) - AAB
Expanding: (2,2,C) - AABABC
Expanding: (6,3,B) - AABABCAABB
Expanding: (10,1,C) - AABABCAABBAC
Expanding: (0,0,) - AABABCAABBAC
Testing It Out
I have kind of danced around this issue until now, but it needs to be said. No compression algorithm can compress every piece of text. Some files are incompressible, and some can even grow - even when using a properly implemented algorithm! And the Lempel Ziv algorithms are no exception. Files below a certain length, or suitable lacking in repetition will often times be larger than they would be had they not been encoded at all.
void calculateCompressionRatio(string filename) {
auto slength = filesystem::file_size(filesystem::path(filename));
auto flength = filesystem::file_size(filesystem::path(filename + ".zz"));
cout<<"Starting size: "<<slength<<" bytes"<<endl;
cout<<"Ending size: "<<flength<<" bytes"<<endl;
cout<<(1 - ((double)flength/(double)slength))<<" compression ratio."<<endl;
}
int main(int argc, char* argv[]) {
if (argc < 3) {
return 0;
}
if (argv[1][0] == 'c') {
compressFile(argv[2]);
calculateCompressionRatio(argv[2]);
} else if (argv[1][0] == 'd') {
uncompressFile(argv[2]);
}
}As an example, lets take a look at two different files. The first file is the Poem "Ozymandis", which is a relatively short poem with no real repetition to speak off.
I met a traveller from an antique land,
Who said — "Two vast and trunkless legs of stone
Stand in the desert Near them, on the sand,
Half sunk a shattered visage lies, whose frown,
And wrinkled lip, and sneer of cold command,
Tell that its sculptor well those passions read
Which yet survive, stamped on these lifeless things,
The hand that mocked them, and the heart that fed;
And on the pedestal, these words appear:
My name is Ozymandias, King of Kings;
Look on my Works, ye Mighty, and despair!
Nothing beside remains. Round the decay
Of that colossal Wreck, boundless and bare
The lone and level sands stretch far awayWhen we run this file through lz77 it will actually grow, as can be seen from the beginning and starting sizes of the file:
max@MaxGorenLaptop:~/simple_lz$ ./lz c ozymandias.txt
Starting size: 640 bytes
Ending size: 774 bytes
-0.209375 compression ratio.
max@MaxGorenLaptop:~/simple_lz$The second file is the poem "The charge of the light brigade", which is quite a bit longer. It is comprised of multiple stanzas and contains many repeated phrases.
I
Half a league, half a league,
Half a league onward,
All in the valley of Death
Rode the six hundred.
“Forward, the Light Brigade!
Charge for the guns!” he said.
Into the valley of Death
Rode the six hundred.
II
“Forward, the Light Brigade!”
Was there a man dismayed?
Not though the soldier knew
Someone had blundered.
Theirs not to make reply,
Theirs not to reason why,
Theirs but to do and die.
Into the valley of Death
Rode the six hundred.
III
Cannon to right of them,
Cannon to left of them,
Cannon in front of them
Volleyed and thundered;
Stormed at with shot and shell,
Boldly they rode and well,
Into the jaws of Death,
Into the mouth of hell
Rode the six hundred.
IV
Flashed all their sabres bare,
Flashed as they turned in air
Sabring the gunners there,
Charging an army, while
All the world wondered.
Plunged in the battery-smoke
Right through the line they broke;
Cossack and Russian
Reeled from the sabre stroke
Shattered and sundered.
Then they rode back, but not
Not the six hundred.
V
Cannon to right of them,
Cannon to left of them,
Cannon behind them
Volleyed and thundered;
Stormed at with shot and shell,
While horse and hero fell.
They that had fought so well
Came through the jaws of Death,
Back from the mouth of hell,
All that was left of them,
Left of six hundred.
VI
When can their glory fade?
O the wild charge they made!
All the world wondered.
Honour the charge they made!
Honour the Light Brigade,
Noble six hundred!When we use lz77 on this file, the results are quite different. This time we have managed to reduce the file size by 30%, which is a fairly decent overall savings.
max@MaxGorenLaptop:~/simple_lz$ ./lz c light_brigade.txt
Starting size: 1576 bytes
Ending size: 1099 bytes
0.302665 compression ratio.
max@MaxGorenLaptop:~/simple_lz$ So there you have it, the venerable lz77 compression algorithm. In a future post I will cover the lz78 algorithm, which is very similar but uses pairs instead of triples, and an explicit dictionary instead of a sliding window. Until Next time, Happy Hacking!
Leave A Comment