Fast sub string searching in amortized O(d) with Suffix Trees

There are a lot of ways to test if a string is contained within another string. Unfortunately, when it comes to searching in strings the algorithms are either incredibly complex and sensitive to implementation details (looking at you KMP) or just downright slow.

In a previous article I went over a technique for accomplishing this in amortized O(nlogn) using suffix arrays. In this post we will return to the task of searching for a string within a string, but this time using a tree based approach to bring the expected complexity down to O(d) where d is the number of characters in the substring. If you have not read my posts on Suffix Arrays or Prefix Tries, I’d recommend reading them first, as this post builds off of techniques which they cover.

Suffix Trees

Suffix trees are, confusingly, a type of prefix trie. Because of the large amount of data involved in constructing one, often times a compressed trie is utilized. For the sake of brevity, I will be using the non-compressed variant.

template <int RADIX = 256>
class SuffixTrie {
    private:
        struct node {
            char c;
            bool eos;
            node* next[RADIX];
            node(char _c, bool e) { 
                c = _c; eos = e;
                for (int i = 0; i < RADIX; i++)
                    next[i] = nullptr;
            }
        };
        node *root;
        int n;
    public:
        SuffixTrie(string s);
        ~SuffixTrie();
        void insert(string s);
        bool contains(string s);
};

The main difference between Suffix Trees and Prefix Tries is a) how they are initially constructed, and b) the way the search procedure works. Prefix tries can be used in a manner similar to symbol tables, in that during their lifetime data may be inserted or removed at any time. A suffix tree is generated all at once, this is considered the “pre-processing” phase of the algorithm, which allows the search operation to be performed in O(d).

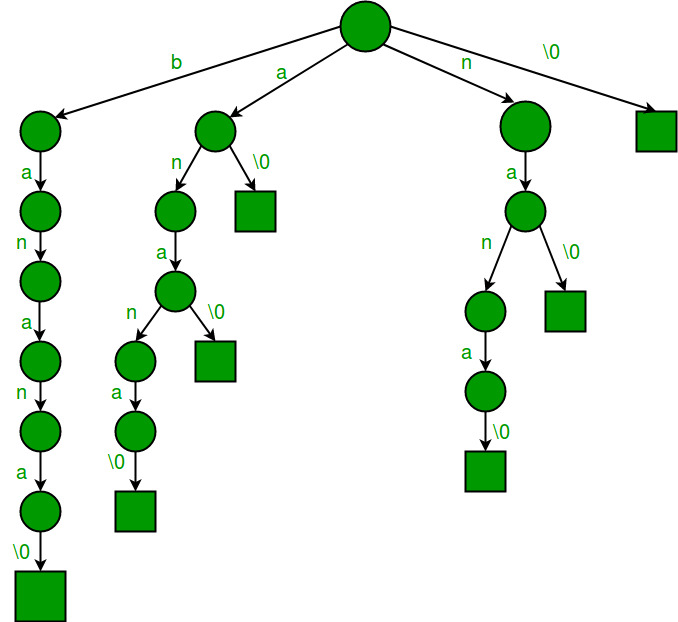
The insert method is exactly the same as for a standard prefix trie, (note that blank spaces are not inserted):

 void insert(string s) {
     node *x = root;
     for (char c : s) {
          if (c == ' ')
               continue;
          if (x->next[c] == nullptr) {
               x->next[c] = new node(c, false);
          }
          x = x->next[c];
     }
     x->eos = true;
} 

Construction of the tree its self initially proceeds in the way as building a suffix array. That is, the piece of text to be searched is used to generate a list of all suffixes of the string. These suffix strings are then inserted one by one in to the tree, in the following example this is done by passing the string to the constructor:

SuffixTrie(string s) {
      n = 0;
      root = new node('#', false);
      for (int i = 0; i < s.size(); i++) {
          insert(s.substr(i, s.size() - i));
      }
} 

The search method has a subtle but very important difference. Part of the node structure of our trie is the eos – end of string – flag, which is set to true for the node storing the last character of a string. In the standard implementation of a prefix trie algorithm, if we reach the end of our search string, but the node we end on is not flagged as end of string, then we return a failure state, because even though the terms matched, the search term did not end in the same position as the text being searched: partial matches don’t count. But for a suffix tree, a partial match is exactly what were aiming for, because we want to know if the string we are searching for is contained within the string that we’re searching for! Thus, all we need to do is remove the end of string check from the normal prefix trie search algorithm:

bool contains(string s) {
      node* x = root;
      for (char c : s) {
          if (x->next[c] == nullptr)
              return false;
          x = x->next[c];
      }
      return true;
  } 

This algorithm is beautiful in it simplicity: we walk the search string as we traverse the trie, at each node we check if the current node has a child for the character being examined. If it doesn’t, the string isn’t in the trie and the search is over. If we reach the end of the search string however, then we know that the string we are searching for is contained within the text:

#include <iostream>
#include "suffixTrie.hpp"
using namespace std;
  
int main(int argc, char* argv[]) {
    string msg = "A Software Engineering Space";
    SuffixTrie st(msg);
    string strs[] = {"Engine", "warez", "poose", "ring", "plane", "war"};
    for (string str : strs) {
        cout<<"Searching for: "<<str<<" in \'"<<msg<<"\': ";
        if (st.contains(str)) {
            cout<<"Found!\n";
        } else {
            cout<<"Not Found.\n";
        }
    }
    return 0;
} 
 
 max@MaxGorenLaptop:/mnt/c/Users/mgoren/AStar$ g++ suffixTrie.cpp -o suffixTrie
 max@MaxGorenLaptop:/mnt/c/Users/mgoren/AStar$ ./suffixTrie
 Searching for: Engine in 'A Software Engineering Space': Found!
 Searching for: warez in 'A Software Engineering Space': Not Found.
 Searching for: poose in 'A Software Engineering Space': Not Found.
 Searching for: ring in 'A Software Engineering Space': Found!
 Searching for: plane in 'A Software Engineering Space': Not Found.
 Searching for: war in 'A Software Engineering Space': Found!
 max@MaxGorenLaptop:/mnt/c/Users/mgoren/AStar$

Perfect!

So there you have it, fast string searching using suffix tries. Until next time friends, Happy Hacking!