Evaluating S-Expressions

mgcadmin 14-10-2023

S-Expressions are an interesting notation for representing expressions. Taking the form of nested lists prefixed with an operator, they are most recognizable as the syntax of the various Lisp programming languages. Their somewhat alien appearance, and notoriously judicious use of parentheses is quickly offset however by their power and utility once properly acquainted with them.In this post I will go over a little bit of what S-expressions are, how they're used, and how to evaluate them.

What is an S-expression?

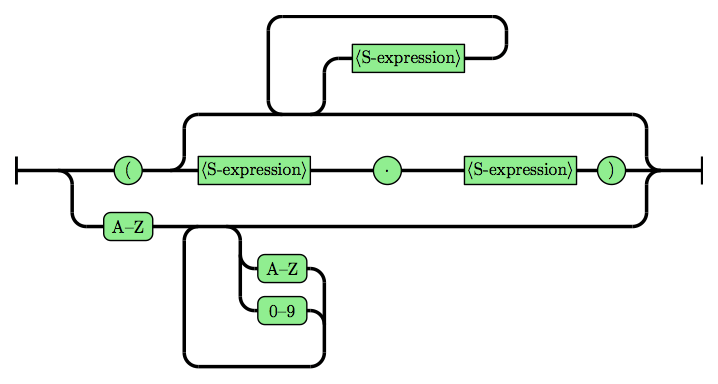
S-expressions, like any other type of expression are comprised of operators and operands. What makes S-expressions different, is that we evaluate them by applying the operator to a list of operands as opposed to having a binary operators act on 2 values.

In a "normal" expression, be it in prefix, postfix, or infix notation, an operator acts on two operands, hence the name binary operator. Put differently, 2 + 2 is a valid infix expression, 2 2 +, is a valid post fix expression, but what about 2 + 2 2? or 2 2 2 + ? Obviously these aren't valid: we're missing information so that not all terms have an associated operator. It isn't hard to see how one might think you can evaluate S-Expressions like prefix expressions, but despite the visual similarity, they are not equivalent and cannot be treated as such.

Part of what differentiates S-expressions from parenthesized-prefix-expressions (say that ten times fast) is that (+ 2 2 2) is a perfectly valid S-expression, it evaluates to 6. Another property of S-expressions is that they can also be nested. Just as (+ 2 2 2) evaluates to six, so does (+ 1 (+ 1 (- 5 3) 2)) also evaluates to 6, or (/ 2 (+ 2 2)) evaluates to 2. So now that we know what S-expressions are, how to we evaluate them?

Evaluating S-Expressions

An S-Expression follows a defined syntax, which is as follows:

(operator <operand list>)

S-Expressions are also recursive in that a member of the operand list, can be an S-Expression, which is evaluated and the value returned being used in the outer expression. In this way, S-Expressions have scope.

(operator <operand operand (operator <operand list>) operand>)

S-Expressions can nest infinitely deep, and can be used for representing very complex calculations. Despite this, there is a straight forward algorithm for their evaluation, which I have laid out in the following pseudo code.

Eval(string expression):
    Let S be a stack of integers
    Let i = 0
    Let op be an operator symbol
    while i < expression.length: 
        if expression[i] == operator:
           op = expression[i]
           i = i + 1
        if expression[i] is a number:
           S.push(expression[i])
           i = i + 1
        if expression[i] is '(':
           Let p = index of next ')'
           Let innerexpr = expression.substring(i, p)
           Let val = Eval(innerexpr)
           S.push(val)
           i = p
         if expression[i] is ')':
           Let result = apply(op, S)
           S.push(result);
           i = i + 1;
    Return S.pop()

Apply(operation, Stack):
     result = Stack.pop();
     while (Stack is not empty):
         result = Stack.pop() <operation> result
     return result             

Each call to Eval will only evaluate one set of parentheses, which is the outer most pair. Nested expressions are handled by recursively calling Eval on them, and their evaluated value used in their place.

Eval works by iterating over the expression position by position, examining what each member of the expression is, and determines what action take. Once the operator for the list being evaluated is determined, the algorithm then processes the operand list.

If the operand is a number, it pushes it onto a value stack, which holds the values of the operand list until we are ready to process them.

If the current position in the expression string is an opening parentheses, then this member of the operand list is a nested expression, and so Eval is recursively called on the expression, and its result pushed to the value stack.

If the current position in the expression string is a closing parentheses, then we are ready to evaluate the current scope, so we call the apply procedure with the value stack and operator as arguments.

Apply works by initially setting a value to the first item on the stack, and then continued to perform the operation passed to it on that value, and the next item on the stack until the stack is empty. An easy way to think of this is an accumulator. You are accumulating the result of performing the operation on the top value of the stack and the previous result.

A Java Implementation

I know that was a little long winded, however its really not very complicated and hopefully i explained it well enough that this code makes sense without extensive commentary. I find this algorithm to be one of those pieces of code that practically writes itself.

import java.util.List;
import java.util.Set;
import java.util.Stack;

public class SExpressionEvaluator {
    private Set<Character> ops;
    private int depth;
    private boolean beQuiet;
    SExpressionEvaluator(Boolean quiet) {
        beQuiet = quiet;
        depth = 0;
        ops = Set.of(Character.valueOf('+'), Character.valueOf('-'), Character.valueOf('/'), Character.valueOf('*'));
    }

    private Integer apply(Character opChar, Stack<Integer> vals) {
        onEntrance("apply", opChar.toString());
        Integer result = vals.pop();
        while (!vals.isEmpty()) {
            switch (opChar) {
                case '+':
                    result += vals.pop();
                    break;
                case '-':
                    result = vals.pop() - result;
                    break;
                case '*':
                    result *= vals.pop();
                    break;
                case '/':
                    result = vals.pop() / result;
            }
        }
        onExit("apply", String.valueOf(result));
        return result;
    }

    public Integer eval(String exp) {
        onEntrance("eval", exp);
        if (exp.charAt(0) != '(') {
            System.out.println("All S-expressions must be enclosed in parentheses");
            return -1;
        }
        Stack<Integer> vals = new Stack<Integer>();
        Character op = 'p';
        for (int i = 1; i < exp.length(); i++) {
            int lpos = i, rpos = i;
            if (ops.contains(exp.charAt(i))) {
                op = exp.charAt(i);
            } else if (exp.charAt(i) == '(') {
                int parenCount = 0;
                while (rpos < exp.length()) {
                    if (exp.charAt(rpos) == '(') {
                        parenCount++;
                    } else if (exp.charAt(rpos) == ')') {
                        if (--parenCount == 0) {
                            rpos++;
                            break;
                        }
                    }
                    rpos++;
                }
                vals.push(eval(exp.substring(lpos, rpos)));
                onAction("push", vals.peek().toString());
            } else if (exp.charAt(i) == ')') {
                vals.push(apply(op, vals));
                onAction("push", vals.peek().toString());
                rpos++;
            } else if (Character.isDigit(exp.charAt(rpos))) {
                while (rpos < exp.length()) {
                    if (Character.isDigit(exp.charAt(rpos)))
                        rpos++;
                    else
                        break;
                }
                vals.push(Integer.parseInt(exp.substring(lpos, rpos)));
                onAction("push", vals.peek().toString());
                rpos--;
            }
            i = rpos;
        }
        onExit("eval", String.valueOf(vals.peek()));
        return vals.pop();
    }

    private void onEntrance(String fname, String fargs) {
        if (beQuiet)
            return;
        ++depth;
        indentDepth();
        System.out.println(" -> " + fname + "(" + fargs + ")");
    }
    private void onExit(String fname, String result) {
        if (beQuiet)
            return;
        indentDepth();
        System.out.println(" <- " + fname + ", " + result);
        --depth;
    }
    private void onAction(String actionName, String args) {
        if (beQuiet)
            return;
        indentDepth();
        System.out.println("  * " + actionName + ": " + args);
    }
    private void indentDepth() {
        for (int i = 0; i < depth; i++) System.out.print("  ");
    }
}

I included two output modes, a "be quiet" mode, which simply performs the calculation and returns the result, and a verbos mode, which gives a traces of the evaluation, verbose mode is obtained by passing "false" to the constructor:

public class Example {  
     public static void main(String[] args) {
        SExpressionEvaluator interp = new SExpressionEvaluator(false);
        List<String> exprs = List.of("(+ 33 232)", "(/ (* 4 2 3) 2)", "(+ 1 2 3 4)", "(* (+ 2 3) (+ 1 (+ 1 1) 2)))");
        for (String str : exprs) {
            System.out.println(interp.eval(str));
        }
        
    }
}

When a method is called, its output is prefixed by a '->', followed by the method name, and the arguments passed to it. When an action is being performed in that method, its output its prefixed by a '*', followed what action is happening. When a method exits, its output is prefixed by a '<-', followed by the method name, and its result. The amount of indentation indicates the level of recursion.

[Running] cd "/home/max/" && javac Example.java && java Example
   -> eval((+ 33 232))
    * push: 33
    * push: 232
     -> apply(+)
     <- apply, 265
    * push: 265
   <- eval, 265
265
   -> eval((/ (* 4 2 3) 2))
     -> eval((* 4 2 3))
      * push: 4
      * push: 2
      * push: 3
       -> apply(*)
       <- apply, 24
      * push: 24
     <- eval, 24
    * push: 24
    * push: 2
     -> apply(/)
     <- apply, 12
    * push: 12
   <- eval, 12
12
   -> eval((+ 1 2 3 4))
    * push: 1
    * push: 2
    * push: 3
    * push: 4
     -> apply(+)
     <- apply, 10
    * push: 10
   <- eval, 10
10
   -> eval((* (+ 2 3) (+ 1 (+ 1 1) 2))))
     -> eval((+ 2 3))
      * push: 2
      * push: 3
       -> apply(+)
       <- apply, 5
      * push: 5
     <- eval, 5
    * push: 5
     -> eval((+ 1 (+ 1 1) 2))
      * push: 1
       -> eval((+ 1 1))
        * push: 1
        * push: 1
         -> apply(+)
         <- apply, 2
        * push: 2
       <- eval, 2
      * push: 2
      * push: 2
       -> apply(+)
       <- apply, 5
      * push: 5
     <- eval, 5
    * push: 5
     -> apply(*)
     <- apply, 25
    * push: 25
   <- eval, 25
25

[Done] exited with code=0 in 1.517 seconds

What's Next

From here the code is very expandable, its relatively straight forward to add things like named variables, additional operators, etc. You can think of it as a very basic Lisp. For a look at the idea's shown here taken a bit further as discussed I encourage you to check out my project, MGCLisp!

Until next time, Happy Hacking!

---