Data Structure Visualization Revisited

mgcadmin 26-10-2023

As I've mentioned in previous posts I am keenly interested in methods of generating visual representations of data structures, and data movement as algorithms progress. I recently revisited the Idea of generating images of various linked data structures as they are generated.

I've been looking for the right library to handle the graphics side of things, and believe I have found a winner in SFML, as it is opensource, well documented, and has good C++ support. Another thing I like about SFML is that it is very lightweight. It allows me as the developer to focus on what I want to accomplish with the library instead of the library its self.

In Sedgewick's "Algorithms in C++" (2nd ed.) the chapter on tree's briefly mentions that you can determine what the x/y coordinates for the nodes of a binary search tree by modifying the in-order traversal algorithm. Goodrich & Tamassia also discuss this method of drawing binary search tree's in their book "Data Structures and Algorithms in C++".

 struct node {
    char info;
    node* left;
    node* right;
};

struct Point {
    int x, y;
    char label;
    Point(int x_ = 0, int y_ = 0, char label_ = 'a') {
        x = x_; y = y_; label = label_;
    }
};

vector<Point> points;
int X, Y;
void visit(node* x) {
    Y++;
    if (x != nullptr) {
        visit(x->left);
        points.push_back(Point(++X,Y,x->info));
        visit(x->right);
    }
    Y--;
} 

It is a rather straight forward, and also quite elegant algorithm. The problem is that it only does half the job! We still need a method to generate the edges otherwise we end up with the following:

Not bad - but not great either. In order to create the edges, we are going to add an additional step to the in order traversal: we are going to save the coordinates of each node in a hash table using that nodes key as the key to the hash table. This might seem redundant, but you'll see why I do this in a moment.

unordered_map<char, pair<int, int>> edges;
vector<Point> points;
int X, Y;
void visit(node* x) {
    Y++;
    if (x != nullptr) {
        visit(x->left);
        points.push_back(Point(++X,Y,x->info));
        edges[x->info] = make_pair(X, Y);
        visit(x->right);
    }
    Y--;
}

Now once we have the coordinates of each node, we perform a breadth first traversal of the tree. In SFML, a Line is drawn by creating an array of Vertex's. Using the hash table we built in the previous traversal, we now obtain the endpoints for each edge by getting the coordinates of the node being visited and its children.

      void markEdges(nodeptr h) {
            queue<nodeptr> fq;
            fq.push(h);
            while (!fq.empty()) {
                h = fq.front();
                fq.pop();
                if (h != nilmarker) {
                    auto v = coordsAndKeys[h->key];
                    if (h->left != nilmarker) {
                        auto u = coordsAndKeys[h->left->key];
                        sfLine line = new sf::Vertex[2] { 
                            sf::Vertex(sf::Vector2f(v.first+5, v.second+5)), sf::Vertex(sf::Vector2f(u.first+5, u.second+5))
                        };
                        line[0].color = sf::Color::Black;
                        line[1].color = sf::Color::Black;
                        edges.push_back(line);
                    }
                    if (h->right != nilmarker) {
                        auto u = coordsAndKeys[h->right->key];
                        sfLine line = new sf::Vertex[2] { 
                            sf::Vertex(sf::Vector2f(v.first, v.second)), sf::Vertex(sf::Vector2f(u.first, u.second))
                        };   
                        line[0].color = sf::Color::Black;
                        line[1].color = sf::Color::Black;                   
                        edges.push_back(line);
                    }
                    fq.push(h->left);
                    fq.push(h->right);
                }
            }
        } 

Once we have the coordinates of everything we want to display, all that's left to do is render them to the window with SFML, which also provides a very simple API for saving the tree's as a file.

     void drawTree() {
            sf::RenderWindow window(sf::VideoMode(1790,500), "Self-Balanacing Binary Search Trees");
            while (window.isOpen()) {
                sf::Event event;
                while (window.pollEvent(event)) {
                    if (event.type == sf::Event::Closed) {
                        sf::Image screen = window.capture();
                        screen.saveToFile("tree.jpg");
                        window.close();
                    }
                }
                window.clear(sf::Color::White);
                for (auto edge: edges) {
                    window.draw(edge,2,sf::Lines);
                }
                for (auto node : nodes) {
                    window.draw(node);
                }
                window.display();
            }
        }

Using the above code (A link to the full implementation is at the bottom) I was able to produce the following images of AVL Trees, Red Black Trees and Left Leaning Red Black Tree's, as well as the unbalanced binary search tree at the top of the post.

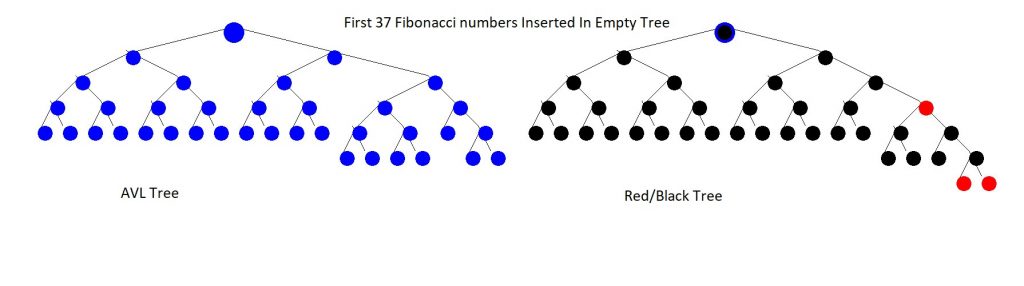
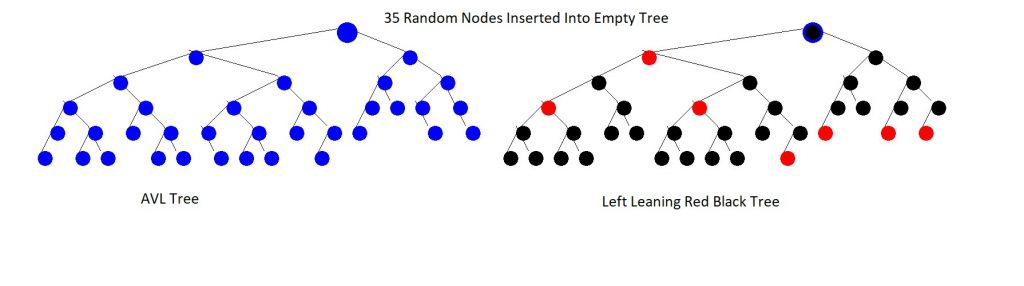
The code for the visualizer, as well as the various binary search tree's are available on my GitHub: https://github.com/maxgoren/TreeVisualizer

 

---