Heaps are ubiquitous in computer science. If you need the minimum, or maximum of a collection, few choices are better than a heap for getting them. Heap-forming algorithms are the foundation of many different algorithms and data structures. From heapsort to priority queues, to huffman coding, heaps really are everywhere.
Heaps make use of two fundamental operations: siftup and siftdown, which take an index of a position in a heap in place it in a heap ordered position. When an entire collection is placed in heap order, its called heapifying the collection.
template <class T>
void siftup(T a[], int n, int k) {
T v = a[k];
while (k > 0 && a[k/2] <= v) {
a[k] = a[k/2];
k = k/2;
}
a[k] = v;
}
template <class T>
void siftdown(T a[], int n, int k) {
T v = a[k];
while (2*k < n) {
int j = k+k;
if (j < n && a[j] < a[j+1]) j++;
if (v >= a[j]) break;
a[k] = a[j]; k = j;
}
a[k] = v;
}
When the a binary heap is used as an explicit data structure, as is the case with a priority queue, it is often built using siftup when inserting a value and siftdown upon removing the root. And so when heapsort was first published, it followed suit.
To siftDown or siftUp?
J. Williams utilized both siftup and siftdown in his original heapsort implementation. It is Robert Floyds “Tree-Sort” that was published a few months later that we know commonly today as heapsort.
Heapsort can generally be separated into two phases:
- The initial “heapifying “of the input array when the collection to be sorted is initially transformed into heap order
- The “pop and maintain” phase which continuously removes the root and placing it in it’s sorted position, followed by the re-heapifying of the unsorted portion of the collection.
void heapsort(int a[], int l, int r) {
int n = r-l;
int *pq = a+l;
//phase 1
makeHeap(pq, n);
//phase 2
while (n > 0) {
exch(pq, 0, n--);
siftdown(pq, n, 0);
}
}
It is the first phase of the algorithm which differs between the two approaches. Williams original implementation builds the heap using siftUp():
void makeHeap_williams(int a[], int n) {
for (int i = 1; i < n; i++)
siftup(a, n, i);
}
Floyds version on the other hand makes uses siftDown(). Notice the difference in both array bounds, and direction of iteration between the two versions.
void makeHeap_floyd(int a[], int l, int r) {
for (int i = n/2; i >= 0; i--)
siftdown(a, n, i);
}
It seems at first glance to be a subtle difference of little importance: they both transform the provided array into heap order, but one goes up and one goes down. The truth of the matter though, is that Floyd’s heapify runs closer to O(n) while Williams version is O(n log n) and that is not a subtle difference.
//The heaps produced in the first phase of both algorithms, and the total //running time of both - Floyd's is more than 2x faster!!
Williams heapify:
98 97 95 94 93 92 78 80 80 82 74 90 36 76 30 78 49 66 70 82 1 3 20 84 19 35 29 14 13 13 5 61 26 42 45 25 24 61 2
Heap Sort completed succesfully in 0.04622
Floyds heapify:
98 97 94 95 93 90 80 80 92 82 66 78 76 30 61 78 49 84 82 61 1 3 74 20 35 36 29 14 13 13 5 19 26 42 45 25 24 70 2
Heap Sort completed succesfully in 0.02129
As you can see, both algorithms build valid heaps, but they don’t build the same heaps, and Floyds version does it much faster. Even at small values of N, its apparent that building the heap bottom up is the clear winner. Why?
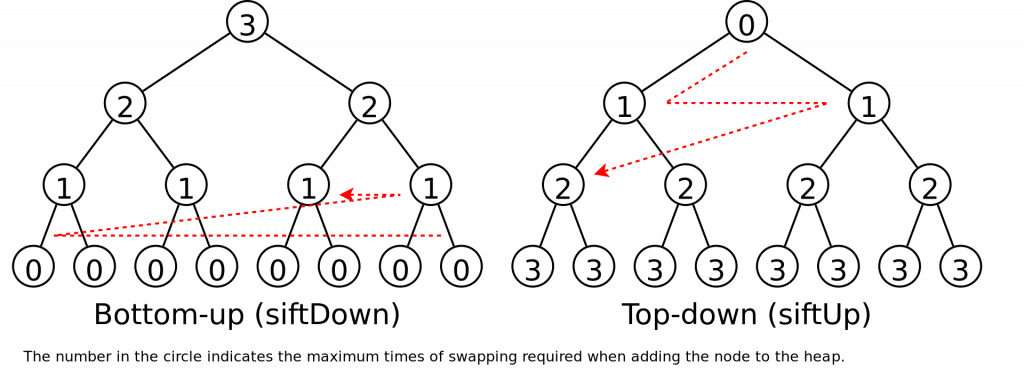Floyd’s version exploits the property that in a complete binary tree, he needed word about the leaf nodes, and thus can get away with making half the number of calls to siftDown() than williams corresponding code makes to siftUp(). But this isn’t the sole cause for such a speed up. siftDown() works buy building many small heaps and merging them together. siftUp() on the otherhand, maintains just one big heap on the unsorted position of the array. It turns out it’s more efficient to have many smaller heaps than one large one.
Further Reading
[1] http://math0.wvstateu.edu/~baker/cs405/code/HeapSort.pdf
[2] https://en.wikipedia.org/wiki/Heapsort
[3] My templated C++ implementation of all algorithms discusses in this post is available on my github
