In-memory B Trees Made Simple

mgcadmin 29-06-2024

As computer architectures continue to evolve, data structures which were once considered well suited for one task may shift to become more applicable for a different task. One example of this is the family of balanced search tree's known as B-Trees. B-Tree's were first introduced in the early 1970's, and have had a long and productive history serving to organize large amounts of data on disk, be it as the index to a database system, or serving as the underlying file system organization at large. However, with the drastic reduction in cost and simultaneous increase in storage capacity of computer memory, B-Tree's have become relevant as an in-memory data structure. This trend can be seen for example with the rust standard library implementation of a sorted dictionary using a modified B-Tree as well as Googles opensource cpp-btree library.

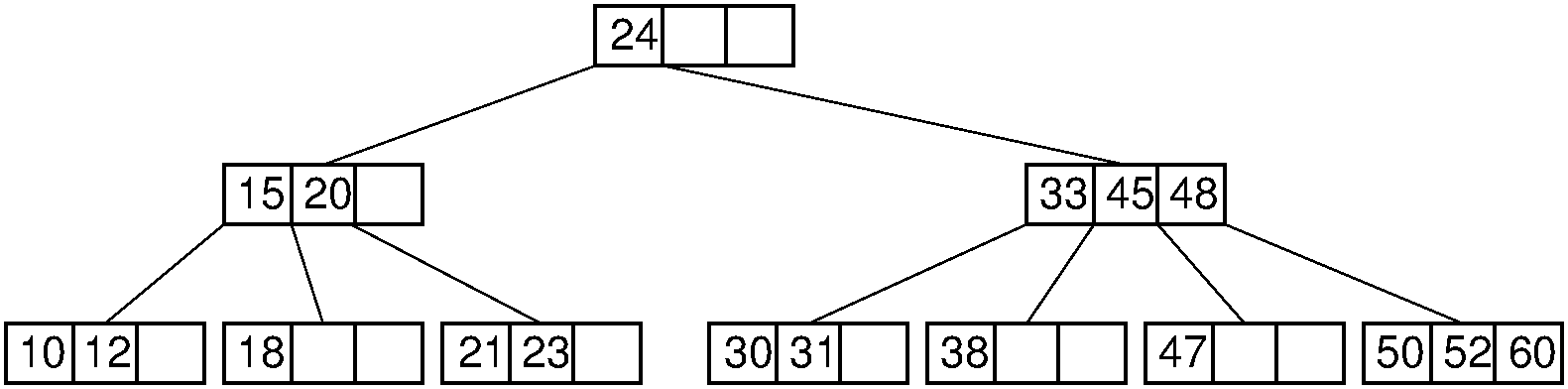
In a previous article I covered bottom up insertion in B+ tree's. While obviously a member of the family of B Trees, they are a quite different data structure with different properties and use cases than the "classical" B Tree I will cover in todays post. Unlike B+ trees whose upper levels serve solely as an index with data held only in their leaf nodes, traditional B Trees store data in both leaf and internal nodes. This is actually more desirable for an in-memory structure as keys in the tree are uniquely paired to their in-node associated value, saving overall space. Red/Black Trees, a data structure I have covered in detail, is its self an abstraction of "classical" B Trees implemented as binary trees.

The B Tree Node Structure

The nodes of a B Tree must have room to store M child pointers, and M-1 Key/Value Pairs. I use a KVPair structure to hold they key/value pairs, but you can also use parallel arrays. The key/value pairs are stored in sorted order which works to maintain the overall search tree property. The child pointers point to nodes whos keys fall in the range between successive keys. One advantage to using the KVPair class, is that when combined with a sentinel dummy node it provides us with a means for gracefully returning from failed search operations in a manner similar to the iterator pattern.

template <class K, class V>
class KVPair;
 
template <class K, class V>
struct bnode {
    KVPair<K,V> data[M-1];
    bnode* next[M];
    int n;
    bool isleaf;
    bnode(bool leaf) {
        isleaf = leaf;
        for (int i = 0; i < M; i++)
            next[i] = nullptr;
    }
};
  
template <class K, class V>
class KVPair {
    private:
        K _key;
        V _value;
        bool _empty;
    public:
        KVPair(K k, V v) {
            _key = k;
            _value = v;
            _empty = false;
        }
        KVPair() { _empty = true; }
        void clear() { 
            _empty = true;
            _key = K();
            _value = V();
        }
        bool operator==(const KVPair& o) const {
            if (_empty && o._empty)
                return true;
            return _key == o._key;
        }
        bool operator!=(const KVPair& o) const {
            return !(*this==o);
        }
        const K& key() const { return _key; }
        V& value() { return _value; }
        bool empty() { return _empty; }
        void setValue(V val) {
            _value = val;
        }
};

Another design choice to consider is how to implement the nodes: plain old structs, or classes. In my post on B+ trees I discussed the utility of the "page" abstraction, where each node is essentially a self contained sorted array based symbol table with the B+ tree class chaining them together into a tree structure. It really boils down to whether you want to take a more procedural vs OOP way of implementing the tree and it's associated structures, and in this case I have opted for the more procedural style. The reason for this is the split operation. In traditional B trees the split method is more complicated than for B+ tree's, and I found it more organizationally consistent to keep all of the algorithmic logic in one class.

Searching And Traversal In B Trees

B Trees - the entire family of B Trees - are based on a deceptively simple concept which can be viewed from several different levels of abstraction. At the heart of all of it are two fundamental properties: the sorted array, and the search tree property. B Tree's are balanced m-way search tree's, who's nodes contain m-1 sorted arrays. They maintain perfect balance, having all of their leaf nodes on the same level while growing laterally and upwards. This is accomplished by a carefully choreographed series of node splits and key promotions. Based on how and when one chooses to perform these node splits leads to the various different B Tree variants.

template <class K, class V>
class BTree {
    private:
        using link = bnode<K,V>*;
        link root;
        int count;
        int levels;
        KVPair<K,V> nullInfo;
        void distributeKeys(link child, link nn, int index);
        void addNodeToParent(link node, link child, int index); 
        void addKVPairToParent(link node, KVPair<K,V> data, int index);
        void split(link node, int index);
        void traverse(link node);
        link search(link node, K key);
        void addKVPair(link node, K key, V value);
        void insert(link x, K key, V value);
    public: 
        BTree();
        void insert(K key, V value);
        bool contains(K key);
        KVPair<K,V>& get(K key);
        int height();
        void show();
};

To introduce the organizational structure of B Trees, I'll start with traversal and search. As I previously mentioned, an important property of B Trees is that they maintain the search tree property, which posits that an in-order traversal of the tree should yield the key's in sorted order. An In order traversal is performed by first recursively traversing a nodes child at index i, before printing the key at index i. Once we have traversed all of the keys in a node, we traverse down the index at size(node.keys) + 1. This is because of our nodes containing M-1 keys and M children.

void traverse(link node) {
     if (node != nullptr) {
        int i = 0;
        while (i < node->n) {
            if (node->next[i] != nullptr)
                traverse(node->next[i]);
            cout<<node->data[i].key()<<" ";
            i++;
        }
        if (node->next[i] != nullptr)
            traverse(node->next[i]);
     }
}

void show() {
     traverse(root);
     cout<<endl;
}

Since the keys are in sorted order we can use binary search to quickly guide us to the correct node when searching. Depending on the degree of your nodes, linear search can also be used and there's some contention as to which my truly be faster on modern architecture. Considering B Tree's should be sized to keep an entire node in a single cache line, binary search should still be faster. Having implemented them both ways I didn't notice much of a difference in performance. What I did fine interesting was that you end up with differently shaped tree's depending on which algorithm you use, as they can select slightly different but still valid partitioning keys.

int findIndex(link node, K key) {
     int l = 0, r = node->n-1;
     while (l <= r) {
           int m = (l+r)/2;
           if (key < node->data[m].key()) r = m - 1;
           else if (key > node->data[m].key()) l = m + 1;
           else return m;
     }
     return l;
} 

KVPair<K,V>& search(link node, K key) {
      if (node == nullptr)
         return nullInfo;
      int index = findIndex(node, key);
      if (key == node->data[index].key())
          return node->data[index];
      return search(node->next[index], key);
} 
 
KVPair<K,V>& get(K key) {
     return search(root, key);
}  

Top Down Insertion

Like most search trees, B Tree's can be constructed either top down or bottom up. We will be implementing an iterative top down insertion algorithm, for the reasons outlined above. I chose to user iteration solely for convenience. Thanks to their normally large branching factor and perfect balance, even truly HUGE B Trees are still fairly short, and thus one can implement the algorithm using recursion without worrying about overflowing the stack.

We will be using a technique called "pre-emptive splitting" where we check the size of the next node as we traverse down the tree towards the insertion location. If the node is full we immediately split the node before even traversing to it. This ensures that every node we move to will have room for an insertion, without the need to do any balancing on the way back up. The only special case is when the root node needs splitting, as this is also the only time the tree grows in height.

void add(K key, V value) {
     if (root->n == M-1) {
         link t = root;
         root = new bnode<K,V>(false);
         root->next[0] = t;
         split(root, 0);
         levels++;
     }
     insert(root, key, value);
} 

After checking the root and handling it's splitting if required, we search down the tree to find the appropriate leaf with which to insert our data. If during the search we encounter a node with the same key we are inserting we simply update its associated value and exit. B Tree's can handle multiple identical keys just fine, but you will need a more complicated search procedure. If the next node we need to go to is full, we split the node, and then adjust our index pointer incase the node to insert to has changed to the new node created during the split. Upon reaching a leaf node, we insert our KVPair with insertion sort.

void addKVPair(link node, K key, V value) {
     int j = node->n;
     while (j > 0 && node->data[j-1].key() > key) {
          node->data[j] = node->data[j - 1];
          j--;
     }
     node->data[j] = KVPair<K,V>(key, value);
     node->n++;
} 

void insert(link x, K key, V value) {
     link node = x;
     while (!isLeaf(node)) {
           int i = findIndex(node, key);
           if (key == node->data[i].key()) {
                node->data[i].setValue(value);
                return;
           }
           if (isFull(node->next[i])) {
                split(node, i);
                if (node->data[i].key() < key)
                   i++;
          }
          node = node->next[i];
     }
     addKVPair(node, key, value);
     count++;
} 

The splitting routines are really the beating heart of the B Tree. Depending on how and when one chooses to split nodes, different variants of the B Tree result, and as it turns out the "traditional" B Tree split routine is actually much more involved than the one used for B+ trees. The reason for this is because the upper levels of B Tree's serve as more than just an index, and thus it is unique Key Value pairs that get promoted to the parent, and subsequently removed from the child. This second step is not necessary in B+ trees, where the upper levels are only used as an index to the correct leaf node where ALL data is stored.

void split(link node, int index) {
      link child = node->next[index];
      link nn = new bnode<K,V>(child->isleaf);
      distributeKeys(child, nn, index);
      addNodeToParent(node, nn, index);
      addKVPairToParent(node, child->data[(M/2)-1], index);
} 

The first step in splitting a node is to create the new node, and distribute the KVPairs and child pointers between them, save for the pair that will be promoted. After that, the newly created node is inserted into the parent of the node it was split from. Finally, the KVPair used as the pivot for partitioning the node is also inserted into the parent node.

 void distributeKeys(link child, link nn, int index) {
            for (int j = 0; j < M/2 - 1; j++)
                nn->data[j] = child->data[j + (M/2)];
            if (!child->isleaf) {
                for (int j = 0; j < M/2; j++) {
                    nn->next[j] = child->next[j+(M/2)];
                }
            }
            nn->n = (M/2) - 1;
            child->n = (M/2) - 1;
}

void addNodeToParent(link node, link child, int index) {
     for (int j = node->n+1; j > index; j--)
         node->next[j] = node->next[j-1];
     node->next[index+1] = child;
}

void addKVPairToParent(link node, KVPair<K,V> kvpair, int index) {
     for (int j = node->n; j > index; j--)
         node->data[j] = node->data[j-1];
     node->data[index] = kvpair;
     node->n++;
}  

We now have the necessary algorithms for inserting and retrieving items from an in memory B Tree. To test the B Tree, I used the sample word files available from here and here to calculate the frequencies of occurrences of words in the text files.

void btree_test(string filename) {
    BTree<string,int> st;
    ifstream in_file(filename);
    if (!in_file.is_open()) {
        cout<<"Couldn't open "<<filename<<" for reading."<<endl;
        return;
    }
    string input;
    auto timestamp1 = std::chrono::steady_clock::now();
    while (!in_file.eof()) {
        in_file>>input;
        auto t = st.get(input);
        if (t.empty()) {
            st.add(input, 1);
        } else {
            st.get(input).setValue(t.value() + 1);
        }
    }
    auto timestamp2 = std::chrono::steady_clock::now();
    auto timing = std::chrono::duration<double, std::milli>(timestamp2 - timestamp1);
    in_file.close();
    cout<<"B Tree"<<endl;
    cout<<"Items: "<<st.size()<<endl;
    cout<<"Height: "<<st.height()<<endl;
    cout<<"key: government, value: "<<st.get("government").value()<<endl;
    cout<<"key: business, value: "<<st.get("business").value()<<endl;
    cout<<"Built: "<<timing.count()<<"ms."<<endl;
} 

int main(int argc, char** argv) {
    btree_test(argv[1]);
    return 0;
}

max@MaxGorenLaptop:~/dsa/btree$ ./tbt words10k.txt 
 B Tree
 Items: 10679
 Height: 4
 key: government, value: 7
 key: business, value: 122
 Built: 70.1517ms.
max@MaxGorenLaptop:~/dsa/btree$

 
max@MaxGorenLaptop:~/dsa/btree$ ./tbt words100k.txt 
 B Tree
 Items: 144256
 Height: 5
 key: government, value: 2549
 key: business, value: 1018
 Built: 1878.68ms.
max@MaxGorenLaptop:~/dsa/btree$ 

And that's it! It is simple, but one must also be careful with promotion of KVPairs to the parent, as it can be a bit tricky to select the correct pivoting key. For example, the above tree actually only works with values of M that are even. The algorithm is unsuitable for implementing a 2-3 tree - the smallest occuring valid B Tree. It can (and does) implement a 2-3-4 tree however, which can be directly compared to a RedBlack Tree to see if the tree is working as expected (it does). Anyway, that's all I've got for today, so until next time, happy hacking!

 

---