Rank-based BST Iterators: No Parent Pointer, No Stack, No Problem

mgcadmin 02-08-2024

It's no secret that I am an iterator pattern fan boy. When it comes to implementing search trees - or any container of which you would like to access the elements one by one and in-place for that matter, the iterator pattern is indispensable. It allows us to hide the containers underlying implementation details, affords us a way to signify search misses without the use of returning NULL or some other "magic" value to signify the item isn't present, and provides a convenient interface for other algorithms to work on the elements of our data structure. It is thus unfortunate that the implementation of iterators for a binary search tree based container can be somewhat of a messy affair.

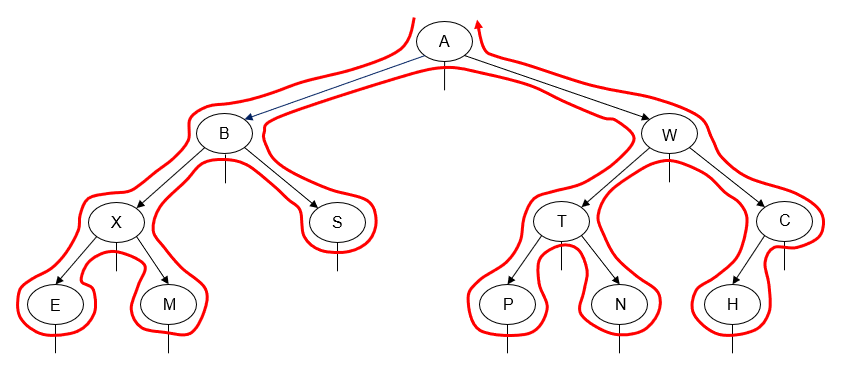
When it comes to implementation the two popular strategies for binary search tree iterators are the use of parent pointers to traverse the tree, or in the absence of parent pointers is the "fat iterator" concept, where one stores the path to the current position in the tree in a stack as well as a pointer to the current node. Both approaches have their negatives, along with vocal opponents to each (welcome to the internet). Parent pointers are disliked for not only the extra space required in each node to accommodate the additional pointer but also the increase in complexity the additional pointer brings to the algorithms, especially those for self-balancing BST's. The so called "fat" iterators are disliked for their larger memory footprint. It should be noted that the implementation used in the C++ standard library is of a parent pointer based Red Black Tree.

In this post I am going to discuss an implementation strategy for binary search tree iterators that that has efficient time complexity and minimal space complexity without the need to rely on either parent pointers or auxiliary data structures. This allows us to use simple recursive algorithms for implementing binary search trees, without sacrificing efficient iteration. In a binary search tree which already supports ordered statistic operations, no additional space is required, otherwise each node needs an additional integer for tracking the side of the subtree rooted at that node. This is still a smaller memory footprint than using parent pointers, with the addition of newly supported operations outside of iteration (rank and select) if one so chooses to make their API's public.

Ordered Statistic Trees, More Useful Everyday!

The "rank" of an element in a binary search tree is the order in which it would appear in an in-order traversal of that tree. To put it another way, if we were to take all of the keys in the tree and place them in an array in sorted order, their rank would be the index of their position in the array. As mentioned above, we can obtain the rank of a node by adding a variable to track the size of the subtree rooted at that node. A leaf node has a size of 1, as it is the only member in it's tree, as such the empty child pointers have a size of 0.

template <class K, class V>
struct node {
    KVPair<K,V> info;
    int size;
    bool color;
    node* left;
    node* right;
    node(K k, V v) : info(k, v), size(1), color(red), left(nullptr), right(nullptr) { }
};

int size(node* x) {
    return (x == nullptr) ? 0:x->size;
}

Upon inserting a new node we update the value of each nodes size counter as the stack unwinds in order to keep the values accurate.

link putRB(link h, K k, V v) {
     if (h == nullptr) {
          count++;
          return new node(k, v);
     }
     if (isRed(h->left) && isRed(h->right)) 
         h = flipColors(h);
     if (k < h->info.key()) h->left = putRB(h->left, k, v);
     else h->right = putRB(h->right, k, v);
     h->n = 1 + size(h->left) + size(h->right);
     return balance(h, true);
}   

Similarly, if the tree we are implementing the iterator for uses balancing algorithms, you must be careful to update the size counters after performing any rotations in the tree as well. For the examples I am using a red black tree, and so we will update the nodes size counts at the same time we update their colors during rotations. It is not necessary to use a self balancing binary search tree, however doing so means that the increment operation for the iterator has a worst case performance guarantee of O(log n) instead of O(h).

link rotL(link h) {
      link x = h->right; h->right = x->left; x->left = h;
      fixHeightAndColor(h, x);
      return x;
}  
 
link rotR(link h) {
      link x = h->left; h->left = x->right; x->right = h;
      fixHeightAndColor(h, x);
      return x;
}  

void fixHeightAndColor(link& x, link& h) {
      x->color = h->color;
      h->color = true;
      x->n = h->n;
      h->n = 1 + size(h->left) + size(h->right); 
}

The last thing we need before we can implement the actual iterator, is to add a method to the tree for the actual selection of a node by rank. This turns out to be a straight forward algorithm that I have covered in previous posts and so will skip the finer details of and skip straight to the implementation.

link select(link x, int rank) {
     if (x == nullptr) return x;
     int curr = size(x->left);
     if (curr > rank) return select(x->left, rank);
     if (curr < rank) return select(x->right, rank - curr - 1);
     return h;
}

And now finally, we are ready to implement our iterator for our tree.

The key observation which lays out the method we will take to implement the iterator is two fold. First, an iterator for a binary search tree should visit each node in the same order as one would during an in-order traversal. And second is the relationship between a nodes rank, and when it appears in an in order traversal as described above. This leads us to the observation that we can simulate an in-order traversal of the tree by selecting each node in the tree according to its rank in increasing order. This gives us a very straight forward method of implementing the actual iterator: the iterator will maintain a pointer to the root of the tree, and a counter variable to track which rank to select, with the increment operator incrementing this counter, and the get operation performing the selection by rank.

By using the same interface for iterator class as the standard library does, we can use C++'s enhanced for loop to iterate over the container. Iterators from the standard library are implemented through operator overloading. All STL compliant iterators must support the following operators

• operator++() - pre increment operator, for advancing the iterators position in the tree
• operator*() - the star operator performs the "get" operation on our iterator, returning the value stored at the current position.
• operator==() - test for equality. is this operator the same as that operator?
• operator!=() - test for inequality. is this operator NOT that operator?

That is of course, only the minimum set needed for a function iterator. Other operators which are often seen depending on the type of iterator are the post increment operator, various decrement operators, algebraic operators for doing the equivalent of pointer math, just to name a few. I personally choose to also implement a non-operator based API for my iterators with the public methods:

• get() - returns the element at the current position
• next() - advances one position to the next in-order element in the tree
• done() - a returns true if there is no more elements to visit, false otherwise.

What can I say? Variety is the spice of life, even for our API's.

 template <class K, class V>
class rankIterator {
    private:
        rbnode<K,V>* tree;
        int pos;
        KVPair<K,V> nullInfo;
        int size(rbnode<K,V>* h) {
            return (h == nullptr) ? 0:h->n;
        }
        KVPair<K,V>& select(rbnode<K,V>* h, int k) {
            if (h == nullptr)
                return nullInfo;
            int t = size(h->left);
            if (t > k) return select(h->left, k);
            else if (t < k) return select(h->right, k-t-1);
            else return h->info;
        }
    public:
        rankIterator(rbnode<K,V>* rootptr, int p) {
            tree = rootptr;
            pos = p;
        }
        bool done() {
            return tree != nullptr && pos >= tree->size();
        }
        KVPair<K,V>& get() {
            return select(tree, pos);
        }
        void next() {
            pos++;
        }
        rankIterator& operator++() {
            ++pos;
            return *this;
        }
        rankIterator& operator++(int) {
            rankIterator it = *this;
            ++it;
            return *this;
        }
        KVPair<K,V>& operator*() {
            return get();
        }
        bool operator==(const rankIterator& oit) const {
            return tree == oit.tree && pos == oit.pos;
        }
        bool operator!=(const rankIterator& oit) const {
            return !(*this==oit);
        }
}; 

Now to use our iterator with C++'s enhanced for loop all that is required to add the appropriate iterators to our tree class. To be specific, we must implement a method named begin() which returns an iterator pointing to the first element in the tree, and a method named end() which returns an iterator pointing to one passed the last element in our binary search tree.

template <class K, class V>
class RedBlackTree {
     //yadda yadda yadda
     rankIterator<K,V> begin() {
          return rankIterator<K,V>(root, 0);
     }
     rankIterator<K,V> end() {
         return rankIterator<K,V>(root, size());
     }
};



void printTree(RedBlackTree<char, char>& rb) {
    for (auto m : rb) {
        cout<<m.key()<<" ";
    }
    cout<<endl;
}

int main() {
    RedBlackTree<char, char> rb;
    string phrase = "aredblacksearchtreeiterator";
    for (char c : phrase) 
        rb.put(c, c, alg);
    
    rb.levelorder();
    rb.preorder();
    printTree(rb); 
    return 0;
}

max@MaxGorenLaptop:~/mgc_common$ ./rb
      h    
     er    
    bels   
   aceekrrt
  aacd…ei.o.rrtt
 …a………………
      ..
 h e b a a a a c c d e e e e r l k i r o s r r r t t t
 a a a a b c c d e e e e e h i k l o r r r r r s t t t
 Valid Red Black Tree.
max@MaxGorenLaptop:~/mgc_common$  

And there you have it, simple binary search tree iterators using rank. That's all for today, so until next time happy hackling!

 

---