Lossless Compression Using Huffman Coding Tries


One of the most ubiqitous algorithms in data compression is Huffman Coding. Developed in 1951 by David Huffman while a student at MIT, Huffman Coding makes use of a special type of binary tree called a huffman coding trie. Every message or file to be encoded has a unique huffman tree, which is used to create unique prefix codes of optimal length. These prefix codes are then used to encode the message being encoded with the least number of bits possible. Every message has a unique encoding based on the tree created from that message. As such, the huffman coding trie used for a particular file must be known in order to decode the file. To account for this, the trie must be serialized and stored in unencoded form with the file. Despite this requirement, the total encoded message + unecoded tree is generally still less than the unecoded message.
In my previous post I discussed the Lempel-Ziv algorithms which achieve compression by reducing the number of bits needed to represent repeated strings. Huffman Coding, which I will be covering in todays post achieves compression by reducing the number of bits used to represent repeated characters. Because of the different ways in which they go about their respective tasks, LZ based algorithms and Huffman Coding are often combined to yield even greater savings than on their own, as exemplified by the DEFLATE algorithm. This property of huffman coding is something quite rare when it comes to lossless compression algorithms, making it incredibly useful.
The Huffman Coding Trie
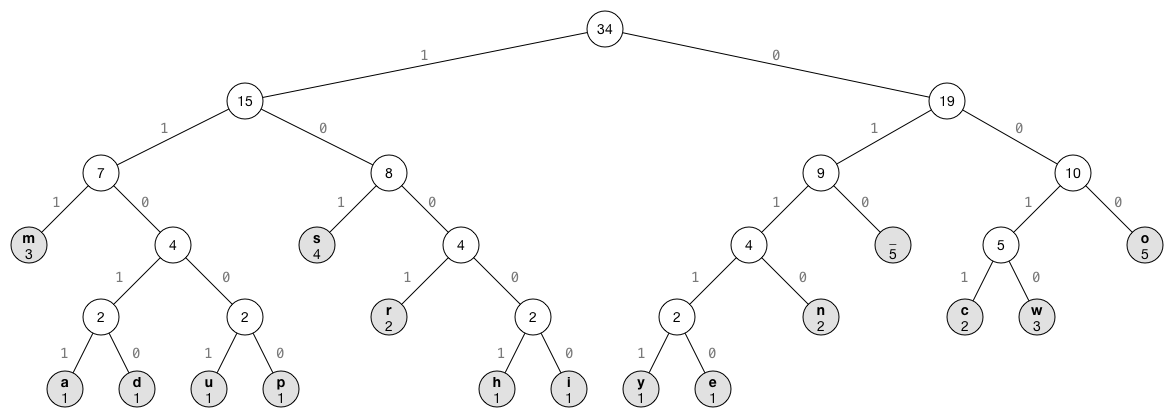
The data structure at the center of this approach is a special form of binary tree called a huffman coding trie. Huffman coding tries are always constructed from the bottom up, with their construction being guided by the frequency of individual characters in the message being encoding. Shannon-Fano coding is a very similar approach which uses tree's built in a top down fashion, resulting in a slightly less efficient encoding.
Being a binary tree, each node contains a left and right pointer, additionally, each node contains a symbol, and frequency count.
struct HuffmanNode {
char symbol;
int frequency;
HuffmanNode* left;
HuffmanNode* right;
HuffmanNode(char s, int p, HuffmanNode* l, HuffmanNode* r) : symbol(s), frequency(p), left(l), right(r) { }
};
using link = HuffmanNode*;The first step in building the trie is to compute the frequency count of the charachters in the file being encoded. We do this by creating a hashtable indexed by char, mapped to our node structure. We iterate over the text and check if it is already in the table. If it is not in the table, we create a new node for that character with a frequency of 1, otherwise we increment the nodes frequency counter.
unodered_map<char, HuffmanNode*> computeFrequencies(StringBuffer data) {
unordered_map<char, link> freq;
while (!data.done()) {
char c = data.get();
if (freq.find(c) == freq.end()) {
freq.emplace(c, new HuffmanNode(c, 1, nullptr, nullptr));
} else {
freq[c]->frequency++;
}
data.advance();
}
return freq;
}Once we have the frequency count of the characters in the file we are ready to start building up the trie. The nodes we just created will form the leaf level of the trie. We construct the trie bottom up by taking the two nodes with lowest frequency counts, and mergeing them by creating a new node whos left and right child pointers point to those nodes, and assigning it a frequency count of the sum of the nodes being merged. This process is repeated until we are left with a single pointer to a node, which is the root of our huffman trie.
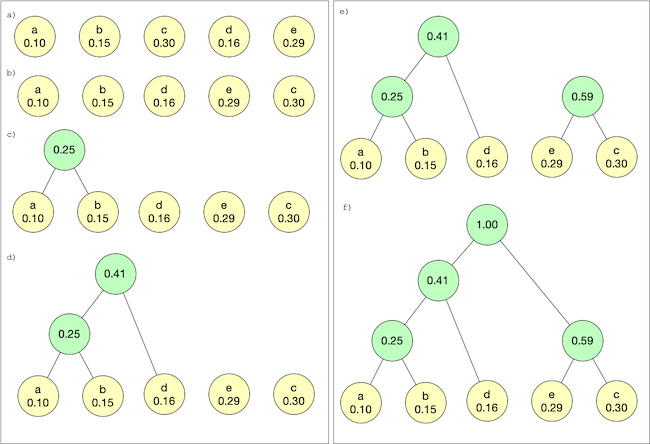
The simplest method of accomplishing this is with a min heap priority queue. We initialize the heap with our leaf nodes, and loop until there is only one item left in the priority queue. At each iteration, we remove the top two entries from the priority queue and merge them as described. Once merged, we place the merged tree back into the priority queue to continue the process.
struct HuffCmp {
bool operator()(HuffmanNode* hna, HuffmanNode* hnb) {
return (hna->frequency > hnb->frequency);
}
};
void HuffEncoder::buildHuffmanTree(StringBuffer data) {
priority_queue<link, vector<link>, HuffCmp> pq;
unordered_map<char, link> freq = computeFrequencies(data);
for (auto it : freq) {
pq.push(it.second);
}
while (pq.size() > 1) {
link a = pq.top(); pq.pop();
link b = pq.top(); pq.pop();
link tmp = new HuffmanNode('&', a->frequency + b->frequency, a, b);
pq.push(tmp);
}
huffmanTree = pq.pop();
}Once the trie hass been constructed, unique codes for each character are obtained by traversing the tree from the node to the leaf. Because each path from root to leave in our tree is unique, each code generated is unique. Well turn now to dicussing generating the codes for encoding our text.
Building The Encoding Table
As mentioned in the previous paragraph, codes are generated according to the path from the root to the leaf representing the code being encoded. The code for each character is generated like this: starting at the root with an empty prefix code, we append a digit for each edge traversed. If we follow the edge to the left child we append a zero to the code, and if we follow the edge to the right child we append 1. When we arrive at the leaf, we have our complete code for the character stored at that leaf.
Once we have generated the tree, our codes will not change, so instead of traversing the trie for every character as we encode it, we will instead do one traversal of our trie, storing each characters code in a hash table. This is easily done with a preorder traversal of the tree.
unordered_map<char, string> encoding;
bool isLeaf(link h) {
if (h == nullptr)
return false;
return (h->left == nullptr && h->right == nullptr);
}
void HuffEncoder::generateEncodingTable(link h, string prefix) {
if (h != nullptr) {
if (isLeaf(h)) {
encoding.insert(h->symbol, prefix);
} else {
generateEncodingTable(h->left, prefix + "0");
generateEncodingTable(h->right, prefix + "1");
}
}
}Encoding The Text
Encoding our text is two step process, first we will convert our text to a binary string, and then convert our binary string to a bitstream. If you want, you can skip the intermediary step and encode straight to BitStream with only slight modification to the following code.
As mentioned, in order to be able to decode the text, we will need to also serialize the trie in its uncompressed form. This is then followed by the number of bits to be decoded, and finally our message. The message is encoded by iterarting over the text to be encoded, and appending the code we generated for that character to our bit string. Once the bit string is written out, we write it to our BitStream - this is when the actual compression takes place.
BitStream squeeze(StringBuffer data) {
string output;
encodeTrie(huffmanTree);
while (!data.done()) {
output += encoding.find(data.get()).value();
data.advance();
}
resultStream.writeInt(output.size(), 8);
for (unsigned char c : output) {
resultStream.writeBit(c == '1');
}
return resultStream;
}Serializing the trie is done by performing a preorder traversal. If the current node is a leaf, we write a 1 to our result BitStream, and then the 8 bit uncombressed character it represents. If the node is an internal node we right a 0 to our result stream. The effect is a compact, but uncompressed binary representation of our trie.
void encodeTrie(HuffmanNode* x) {
if (isLeaf(x)) {
resultStream.writeBit(true);
resultStream.writeChar(x->symbol, 8);
return;
}
resultStream.writeBit(false);
encodeTrie(x->left);
encodeTrie(x->right);
}And with that we have everything we need to compress a file using huffman coding. Having arrived at a BitStream representation, all that is left is to write it to file with our BitStream class's writeStreamToFile() method.
void BitStream::writeStreamToFile(string filename) {
std::ofstream file(filename, std::ios::out|std::ios::binary);
compressed.start();
for (int j = 0; j < compressed.size(); ) {
int i = 0;
unsigned char byte = 0;
while (j < compressed.size() && i < 8) {
if (compressed.readBit()) {
byte |= (1 <<(7-i));
}
i++;
j++;
}
cout<<j<<": "<<byte<<endl;
file.write(reinterpret_cast<const char*>(&byte), sizeof(byte));
}
file.close();
}
void compressFile(string filename) {
StringBuffer sb;
sb.readBinaryFile(filename);
BitStream bits = squeeze(sb);
bits.writeStreamToFile(filename + ".huff");
}As I'm sure you are aware, having encoded the text, the job is only half done. Thankfully, decodeing a file compressed with huffman coding is fairly straight forward.
Decoding Huffman Encoded Text
Decoding our text involves reading our file bytewise into a BitStream. We then read the stream bit wise to reconstruct trie, which is then repeatedly traversed, using our bitstream to guide the traversal. When we arrive at a leaf, we add the symbol at that leaf to the output stream, and restart our traversal from the root. This continues until we have consumed the entire stream, at which point we will have reconstructed our original text.
void uncompress(string infile, string outfile) {
StringBuffer sb;
sb.readBinaryFile(infile);
string uncompressed = unsqueeze(stringBufferToBitStream(sb));
ofstream opf(outfile);
if (opf.is_open()) {
for (unsigned char c : uncompressed) {
opf << c;
}
}
opf.close();
}
BitStream stringBufferToBitStream(StringBuffer compressed) {
BitStream inf;
while (!compressed.done()) {
inf.writeChar(compressed.get(), 8);
compressed.advance();
}
return inf;
}Deserializing the trie is done top-down as we read the bit string. For decoding text frequency counts don't matter: it's the structure of the trie it's self the determines the code, and so we just assign a frequency of zero to all of the nodes.
HuffmanNode* decodeTrie() {
if (trieStream.readBit()) {
return new HuffmanNode(trieStream.readChar(), 0, nullptr, nullptr);
}
link left = decodeTrie();
link right = decodeTrie();
return new HuffmanNode('\0', 0, left, right);
}
string unsqueeze(BitStream encoded) {
string result;
link x = nullptr;
trieStream = encoded;
trieStream.start();
huffmanTree = decodeTrie();
while (!trieStream.done()) {
if (x == nullptr) {
x = huffmanTree;
}
if (isLeaf(x)) {
result.push_back(x->symbol);
x = nullptr;
} else {
x = trieStream.readBit() ? x->right:x->left;
}
cout<<".";
}
if (isLeaf(x)) result.push_back(x->symbol);
return result;
}
And with that, we can now decode our compressed data. As we did with lz77, lets test the implementation on some text.
Test Runs
If you recall from my post on compression with Lempel-Ziv, the length of the file had to be considered as files below a certain size would either not compress, or in some cases could actually grow. With huffman coding, we may encounter uncompressable files - as some data truly just can not be compressed. What we don't have to worry about however is the file growing.
For our tests we will be using the same files that we used to test compression with Lz77, the poems "ozymandias" and "the charge of the light brigade". Up first is Ozymandias:
I met a traveller from an antique land,
Who said — "Two vast and trunkless legs of stone
Stand in the desert Near them, on the sand,
Half sunk a shattered visage lies, whose frown,
And wrinkled lip, and sneer of cold command,
Tell that its sculptor well those passions read
Which yet survive, stamped on these lifeless things,
The hand that mocked them, and the heart that fed;
And on the pedestal, these words appear:
My name is Ozymandias, King of Kings;
Look on my Works, ye Mighty, and despair!
Nothing beside remains. Round the decay
Of that colossal Wreck, boundless and bare
The lone and level sands stretch far away
When subjected to compression with LZ77, the file length of ozymandias.txt actually grew in size. This was the case with lz77 because Ozymandias does not contain many long strings repeated of characters. Seeing as huffman coding exploits completely different properties of the file, let's see what happens when we subject the it to compression with huffman coding.
max@MaxGorenLaptop:~/huffman/textfiles$ ../huffc -ch ozymandias.txt
Starting size: 640 bytes
Ending size: 429 bytes
0.329688 compression ratio.
max@MaxGorenLaptop:~/huffman/textfiles$Whoa! Talk about a difference, instead of growing we actually achieved a 33% reduction in file size! The next file we tested with lz77 was "The charge of the light brigade", which does have many long repeatitions of strings and LZ77 did very well with it.
I
Half a league, half a league,
Half a league onward,
All in the valley of Death
Rode the six hundred.
“Forward, the Light Brigade!
Charge for the guns!” he said.
Into the valley of Death
Rode the six hundred.
II
“Forward, the Light Brigade!”
Was there a man dismayed?
Not though the soldier knew
Someone had blundered.
Theirs not to make reply,
Theirs not to reason why,
Theirs but to do and die.
Into the valley of Death
Rode the six hundred.
III
Cannon to right of them,
Cannon to left of them,
Cannon in front of them
Volleyed and thundered;
Stormed at with shot and shell,
Boldly they rode and well,
Into the jaws of Death,
Into the mouth of hell
Rode the six hundred.
IV
Flashed all their sabres bare,
Flashed as they turned in air
Sabring the gunners there,
Charging an army, while
All the world wondered.
Plunged in the battery-smoke
Right through the line they broke;
Cossack and Russian
Reeled from the sabre stroke
Shattered and sundered.
Then they rode back, but not
Not the six hundred.
V
Cannon to right of them,
Cannon to left of them,
Cannon behind them
Volleyed and thundered;
Stormed at with shot and shell,
While horse and hero fell.
They that had fought so well
Came through the jaws of Death,
Back from the mouth of hell,
All that was left of them,
Left of six hundred.
VI
When can their glory fade?
O the wild charge they made!
All the world wondered.
Honour the charge they made!
Honour the Light Brigade,
Noble six hundred!
Clearly Huffman was on to something back then in 1951, as on the second file we did even better, reaching a compression ratio of .38 for an almost 40% reduction in file size!
max@MaxGorenLaptop:~/huffman/textfiles$ ../huffc -ch light_brigade.txt
Starting size: 1581 bytes
Ending size: 978 bytes
0.381404 compression ratio.
max@MaxGorenLaptop:~/huffman/textfiles$That's what I've got for today. Until next time, Happy Hacking!
-
Composable Linked Digraphs: Yet another NFA Data Structure
-
Improving the Space Efficiency of Suffix Arrays
-
Augmenting B+ Trees For Order Statistics
-
Top-Down AST Construction of Regular Expressions with Recursive Descent
-
Balanced Deletion for in-memory B+ Trees
-
Building an AST from a Regular Expression Bottom-up
-
The Aho, Sethi, Ullman Direct DFA Construction Part 2: Building the DFA from the Followpos Table
-
The Aho, Sethi, Ullman Direct DFA Construction, Part 1: Constructing the Followpos Table
-
Procedural Map Generation with Binary Space Partitioning
-
Exact Match String Searching: The Knuth-Morris-Pratt Algorithm
Leave A Comment