From Parse Trees To AST's: Predictive Parsing using Recursive Descent

mgcadmin 30-03-2024

In the process of turning text into executable programs two of the early transformations that take place are converting said text into a stream of tokens - commonly called "lexing", and transforming this token stream into abstract syntax tree (AST). This second transformation is the result of parsing the token stream. I say it is the result because in between the token stream and the abstract syntax tree lies another structure: the parse tree.

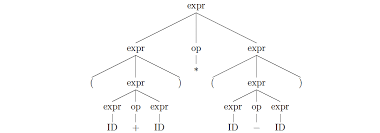
Parse trees are an annotated tree representation of the syntactical structure of the code which is generated implicitly during the parse phase from the activation records of the procedure calls made while parsing. Aside from syntactical structure of the text being parsed, parse trees also represent the derivations of terminals from non-terminals and as such contain much more information than we actually need, and this is where Abstract Syntax Tree's come in to the picture.

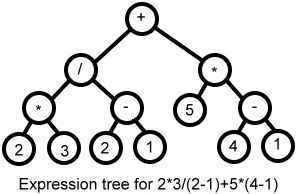
Parse Tree's tell us if the string being read fits together the way we expect it to - in short, parsing checks that the string is syntactically correct. An abstract syntax tree on the other hand, describes what that string should do. An expression tree is a good example of an AST, with internal nodes representing operators (actions) and leaf nodes representing operands. And those derivations I was talking about? They are how we determine to the correct assemblage of the Abstract Syntax Tree with regards to operator precedence.

Lets put together a parser for a simple language to see how this works. Some people choose to implement parsers to generate the abstract syntax tree implicitly, skipping straight to some other intermediate code representation. That however, is not my style - so we're going to need an AST structure

The AST Node

Depending on whether or not you want to allow your if statement to have an else clause or not, our AST node can be either a binary or ternary tree. Our node structure will also have a next pointer which points to its siblings, though it is not a left sibling/right child tree. We will have two types of nodes in our abstract syntax tree: statement nodes and expression nodes, which will be determined by the 'type' flag.

 enum TOKENS {
     ERROR, WHITESPACE, EOFTOKEN,
     DEF, NUMBER, ID,
     PLUS, MINUS, MULTIPLY, DIVIDE,
     ASSIGN, LPAREN, RPAREN, LCURLY, RCURLY,
     LESS, EQUAL, IF, PRINT, LOOP, RETURN, SEMI, COLON, PERIOD, COMA
 };
 enum NodeK {EXPRNODE, STMTNODE};
 enum ExprK {ID_EXPR, OP_EXPR, UOP_EXPR, CONST_EXPR, FUNC_EXPR};
 enum StmtK {PRINT_STMT, IF_STMT, LOOP_STMT, ASSIGN_STMT, DEF_STMT, RETURN_STMT};
 struct ASTNode {
     NodeK kind;
     union { ExprK expr; StmtK stmt; } type;
     struct { TOKENS tokenVal; string stringVal; double doubleVal; } data;
     ASTNode* next;
     ASTNode* left;
     ASTNode* right;
 };
 ASTNode* makeExprNode(ExprK type, TOKENS token, string str);
 ASTNode* makeStmtNode(StmtK type, TOKENS token, string str);

ASTNode* makeExprNode(ExprK type, TOKENS token, string str) {
     ASTNode* node = new ASTNode;
     node->kind = EXPRNODE;
     node->type.expr = type;
     node->data.stringVal = str;
     node->data.tokenVal = token;
     node->left = nullptr;
     node->right = nullptr;
     node->next = nullptr;
     return node;
 }

 ASTNode* makeStmtNode(StmtK type, TOKENS token, string str) {
     ASTNode* node = new ASTNode;
     node->kind = STMTNODE;
     node->type.stmt = type;
     node->data.stringVal = str;
     node->data.tokenVal = token;
     node->left = nullptr;
     node->right = nullptr;
     node->next = nullptr;
     return node;
 }

Our Toy Grammar

We'll keep our language simple but usable to keep the grammar small. It will support variable assignment, if statements (no else), simple loops, a print statement, basic algebraic operators (+, -, *, /), as well as testing for equality (==), and comparison (<). We're only going to support one data type: real numbers, so basically a fancy calculator with conditional branching an iteration.

reserved characters are: + - * / = < : . , ( ) { } := #
reserved words are: if, loop, print
program := stmtlist
stmtlist := statment*
statement := [ exprstmt| ifstmt | loopstmt | assignstmt | print stmt ]; | ;
exprstmt := ( simpleexpr )
ifstmt := if (simpleexpr) { stmtlist }
loopstmt := loop (simpleexpr) { stmtlist }
assignstmt := ID := simpleexpr
printstmt := print simpleexpr
simpleexpr := (expr) { [==|<] (expr) }*
expr := term { +|- term}*
term := var { *|/ var}*
var := ID | NUM | ( simpleexpr ) | -term
ID := string
NUM := real number 

The grammar is constructed in such a way as to allow simple top down parsing with recursive descent. Operator precedence is handled by recursive climbing, which can be seen by taking a closer look at the grammar for expressions at the bottom:

simpleexpr := (expr) { [==|<] (expr) }*
expr := term { +|- term}*
term := var { *|/ var}*
var := ID | NUM | ( simpleexpr ) | - term

Operators with higher precedence occur lower in expression grammar heIrarachy. Unary minus has the highest precedence, followed by division, and as such they occupy the bottom two places. This is because the lower they are in the heriarchy, the sooner they get evaluate after recognizing the terminal token. It is with this knowledge that we can design grammar correctly. Unless you want to end up with a parser that constructs AST's with an incorrect order of operations..

Now that we have our grammar, we can start writing the parser.

Parsing Our Grammar

Parsing is the second step in the compilation/interpretation(translation?) process, the first being lexical analysis. The rest of this post assumes that you have already implemented a lexer for the above grammar. If you have not - or don't want to, one is available on the github repo for this post.

We will be parsing top down, meaning we start from a non terminal at the root of the tree, and build the tree downwards as we encounter the next piece. There is an incredibly straight forward way to do this, assuming you have the correct type of grammar (we do). With a few exceptions, every name on the left side of the grammar will become a procedure, that procedure will then process the grammar rules from the right side of the grammar, recursively calling other procedures as needed, working our way down the grammar rules hence the name Recursive Descent. This is an example of Syntax Directed Translation, and in my opinion is one of the more beautiful concepts from computer science. We will be parsing a stream Tokens represented by the following structure, which is generated by the aforementioned lexer:

struct Lexeme {
     TOKENS tokenVal;
     string stringVal;
     int lineNumber;
     Lexeme(TOKENS t = ID, string sv = "(empty)", int ln = 0) {
         tokenVal = t;
         stringVal = sv;
         lineNumber = ln;
     }
 };

When it comes to implementing a recursive descent parser, we have an important choice to make: will we back track? Backtracking parses are powerful - They can recognize just about any grammar you throw at it. They also have quadratic complexity. Our grammar is simple enough that we can avoid backtracking through a technique called predictive parsing, which has linear complexity. This is accomplished by "guessing" what should come next, instead of blindly trying every choice, and backtracking upon failure. You might think this sounds incredulous, how can a computer "guess" the correct transition? As you'll see in a moment, its actually pretty straight forward.

Implementing a Predictive Parser

Parseing begins with a vector of lexemes, which is the output of the lexer, and when complete will return a fully constructed Abstract Syntax Tree. Much research has been out into parsing. It has been somewhat hyped as to the actual difficulty of parsing programming languages (*cue snarky comment about slaying the dragon of compiler complexity with the sword of LALR Parser Generators). As you shall see, the only thing you really need is to be comfortable with recursion.

class Parser {
        vector<Lexeme> lexemes;
        int lexPos;
        Lexeme current;
        TOKENS lookahead();
        void nexttoken();
        bool match(TOKENS token);
    public:
        Parser();
        ASTNode* parse(vector<Lexeme>& tokens);
        ASTNode* program();
        ASTNode* statementList();
        ASTNode* statement();
        ASTNode* paramList();
        ASTNode* argsList();
        ASTNode* simpleExpr();
        ASTNode* expression();
        ASTNode* term();
        ASTNode* var();
};

The lookahead() method is used to access the current token and nexttoken() advances the tokenstream one position until the tokens have been consumed. match() is used to "accept" the lookahead() token and advance the token stream if it is the token we are expecting, otherwise we have encountered a syntax error. The parseing process beings with a call to parse() which supplies the vector of lexemes that serves as our tokens tream, as well as initializing the lookahead.

ASTNode* Parser::parse(vector<Lexeme>& tokens) {
    lexemes = tokens;
    current = tokens[0];
    lexPos = 0;
    return program();
}

TOKENS Parser::lookahead() {
    return current.tokenVal;
}

void Parser::nexttoken() {
    if (lexPos+1 == lexemes.size()) {
        current = Lexeme(EOFTOKEN, "<fin>", lexPos);
    } else {
        current = lexemes[++lexPos];
    }
}

bool Parser::match(TOKENS token) {
    if (token == current.tokenVal) {
        nexttoken();
        return true;
    }
    if (current.tokenVal != EOFTOKEN) {
        cout<<"mismatched token on line "<<current.lineNumber<<": "<<tokenString[current.tokenVal]<<",expected: "<<tokenString[token]<<endl;
    }
    return false;
}

ASTNode* Parser::parse(vector& tokens) {
     lexemes = tokens;
     current = tokens[0];
     lexPos = 0;
     return program();
 }

ASTNode* Parser::program() {
    ASTNode* node = statementList();
    return node;
}

The statementList() method begins building a list of ASTs each representing a statement ands expressions ("expression" statements are simply expressions, masquerading as statements), strung together by their next pointer - it is quite literally a list of statements..

/*
     Statement List grammar
     statement list := statement*
*/
ASTNode* Parser::statementList() {
     ASTNode* node = statement();
     ASTNode* m = node;
     while (lookahead() != RCURLY && lookahead() != EOFTOKEN) {
         ASTNode* t = statement();
         if (m == nullptr) {
             node = m = t;
             node->next = m;
         } else {
             m->next = t;
             m = t;
         }
     }
     return node;
 }

The call to statement() is where we will begin consuming tokens, a quick glance at the grammar shows we will be handling 8 cases. That's 6 cases for valid statements(if statement, loop statement, assignment, print, and expression statements) 1 case for an empty statement, and an error case. Only one case can be valid, otherwise our grammar would have ambiguity and would be an indication something is wrong. Normally I would break down each case into it's own method, but for grammar as simple as this its not needed.

/* 
grammar for statements  
statement := [ exprstmt| ifstmt | defstmt | loopstmt | assignstmt | print stmt ]; | ; 
*/

ASTNode* Parser::statement() {
     ASTNode* node;
     if (lookahead() == PRINT) {
         match(PRINT);
         node = makeStmtNode(PRINT_STMT, lookahead(), current.stringVal);
         node->left = simpleExpr();
         if (lookahead() == SEMI)
             match(SEMI);
         return node;
     }
     if  (lookahead() == IF) {
         node = makeStmtNode(IF_STMT, lookahead(), current.stringVal);
         match(IF);
         match(LPAREN);
         node->left = simpleExpr();
         match(RPAREN);
         match(LCURLY);
         node->right = program();
         if (lookahead() == RCURLY)
             match(RCURLY);
         return node;
     }
     if (lookahead() == DEF) {
         node = makeStmtNode(DEF_STMT, lookahead(), current.stringVal);
         match(DEF);
         node->data.stringVal = current.stringVal;
         match(ID);
         match(LPAREN);
         node->left = paramList();
         match(RPAREN);
         match(LCURLY);
         node->right = program();
         match(RCURLY);
         return node;
     }
     if (lookahead() == ID) {
         node = makeExprNode(ID_EXPR, lookahead(), current.stringVal);
         match(ID);
         if (lookahead() == ASSIGN) {
             ASTNode* t = makeStmtNode(ASSIGN_STMT, lookahead(), current.stringVal);
             t->left = node;
             node = t;
             match(ASSIGN);
             node->right = simpleExpr();
             if (lookahead() == SEMI)
                 match(SEMI);
             return node;
         }
         if (lookahead() == LPAREN) {
             node->type.expr = FUNC_EXPR;
             node->left = simpleExpr();
             if (lookahead() == SEMI)
                 match(SEMI);
             return node;
         }
     }
     if (lookahead() == LPAREN) {
         node = simpleExpr();
         if (lookahead() == SEMI)
             match(SEMI);
         return node;
     }
     if (lookahead() == RETURN) {
         node = makeStmtNode(RETURN_STMT, lookahead(), current.stringVal);
         match(RETURN);
         node->left = simpleExpr();
         if (lookahead() == SEMI)
             match(SEMI);
         return node;
     }
     cout<<"Unknown Token: "<<current.stringVal<<endl;
     return node;
 }

Statements nodes generally point to expression nodes as can be seen from the code above. As an example, lets take a closer look at the print statement. The grammar of a print statement is the print keyword, followed by an expression, ending in a semi colon. So, if the current token is "print", we consume that token and create a statement node, recording the fact that this statement node represent a print statement. We are now expecting a expression, which we will add to the AST as the print statement nodes left child.

if (lookahead() == PRINT) {
     match(PRINT);
     node = makeStmtNode(PRINT_STMT, lookahead(), current.stringVal);
     node->left = simpleExpr();
     if (lookahead() == SEMI)
         match(SEMI);
     return node;
} 

simpleExpr() is the entry point of our 'precedence ladder', so we assign the result of simpleExpr() anywhere we are expecting an expression.

Parsing Expressions

Recall from earlier that we are using 'precedence climbing' to ensure that our parser builds expression tree's that follow the proper order of operations. This is the reason for the multiple levels of expression grammar. The higher the non terminal appears on the list below, the lower the precedence of the operator.

simpleexpr := (expr) { [==|<] (expr) }*
expr := term { +|- term}*
term := var { *|/ var}*
var := ID | NUM | ( simpleexpr ) | - term
ID := string
NUM := real number 

Once we have the proper ordering to make our recursive calls, our procedures for parsing expressions proceeds much the same as for statements, except that we are creating expression nodes. Otherwise, recognizing tokens and branching based on the current token is the same. Once we hit the var() method, we are consuming terminal symbols, and so are returning the leaf nodes of our tree from var().

ASTNode* Parser::simpleExpr() {
     ASTNode* node = expression();
     if (lookahead() == EQUAL || lookahead() == LESS) {
         ASTNode* t = makeExprNode(OP_EXPR, lookahead(), current.stringVal);
         t->left = node;
         match(lookahead());
         node = t;
         node->right = expression();
     }
     return node;
 }
 
 ASTNode* Parser::expression() {
     ASTNode* node = term();
     while (lookahead() == PLUS || lookahead() == MINUS) {
         ASTNode* expNode = makeExprNode(OP_EXPR, lookahead(), current.stringVal);
         expNode->left = node;
         node = expNode;
         match(lookahead());
         node->right = term();
     }
     return node;
 }
 
 ASTNode* Parser::term() {
     ASTNode* node = var();
     while (lookahead() == MULTIPLY || lookahead() == DIVIDE) {
         ASTNode* expNode = makeExprNode(OP_EXPR, lookahead(), current.stringVal);
         expNode->left = node;
         node = expNode;
         match(lookahead());
         node->right = var();
     }
     return node;
 }

 ASTNode* Parser::var() {
     ASTNode* node;
     if (lookahead() == NUMBER) {
         node = makeExprNode(CONST_EXPR, lookahead(), current.stringVal);
         match(NUMBER);
         return node;
     }
     if (lookahead() == ID) {
         node = makeExprNode(ID_EXPR, lookahead(), current.stringVal);
         match(ID);
         if (lookahead() == LPAREN) {
             match(LPAREN);
             node->type.expr = FUNC_EXPR;
             if (lookahead() != RPAREN)
                 node->left = simpleExpr();
             match(RPAREN);
         }
         return node;
     }
     if (lookahead() == LPAREN) {
         match(LPAREN);
         node = simpleExpr();
         match(RPAREN);
     }
     if (lookahead() == MINUS) {
           node = makeExprNode(UOP_EXPR, MINUS, currnet.stringVal);
           match(MINUS);
           node->left = term();
           return node;
     }
     return node;
 }

Traversing the AST

Once our parsing is complete, traversing the resultant AST plays a central role in several important steps, regardless of if you are compiling or interpreting the code being processed. Dept first traversal is used and proceeds as you would any other tree, though you should be cognizant of the sibling pointers, in order to call the statements in the correct order. Depending on which step of compilation you are performing, you will want to process the nodes in different orders, with post order and pre order traversal being the two most common.

class ASTTracer {
     private:
         int depth;
         void printNode(ASTNode* node);
     public:
         ASTTracer();
         void traverse(ASTNode* node);
 };

ASTTracer::ASTTracer() {
     depth = 0;
 }
 void ASTTracer::traverse(ASTNode* x) {
     depth++;
     for (auto node = x; node != nullptr; node = node->next) {
         if (node != nullptr)
             printNode(node);
         if (node->left != nullptr)
             traverse(node->left);
         if (node->right != nullptr)
             traverse(node->right);
     }
     depth--;
 }
 void ASTTracer::printNode(ASTNode* node) {
     if (node == nullptr) return;
     for (int i = 0; i < depth; i++)         cout<<"  ";     if (node->kind == EXPRNODE) {
         switch (node->type.expr) {
             case ID_EXPR:    cout<<"[ID_EXPR]"<kind == STMTNODE) {
         switch (node->type.stmt) {
             case IF_STMT:     cout<<"[IF_STMT]"<<endl; break;
             case LOOP_STMT:   cout<<"[LOOP_STMT]"<<endl; break;
             case PRINT_STMT:  cout<<"[PRINT_STMT]"<<endl; break;
             case ASSIGN_STMT: cout<<"[ASSIGN_STMT]"<<endl; break;
             case DEF_STMT:    cout<<"[DEF_STMT]"<<endl; break;
             case RETURN_STMT: cout<<"[RETURN_STMT]"<<endl; break;
             default:
                 break;
         }
     }
 }

 

 

---