Bottom up Red/Black Trees: The simplicity of LLRB Trees, with none of the penalty.

mgcadmin 22-01-2024

On my shelf I have books by no less than 7 different authors that contain sections on implementing Red/Black Tree's. Almost all of them begin with an introduction to 2-3-4 tree's. In addition, almost all of them detail algorithms that restructure the tree both top down and bottom up during insertion, or briefly discuss bottom up insertion and then detail top-down algorithms. What is perhaps the most widely known version, which appears in CLRS, is an overly-complex iterative implementation requiring parent pointers to perform it's bottom up balancing.

In response to this perceived complexity, both AA trees and Left-Leaning Red/Black trees were introduced, which simplified their implementations by enforcing asymmetry in their balancing. What do I mean by "enforcing asymmetry"? In a "Traditional" red black tree, a red node can appear as either a left or right child of a black node - or even both! In a "Left Leaning Red/Black Tree" however, a red node can only occur as the left child of a node. AA tree's, an earlier adaptation of Red/Black trees perform this same trick, except slanting to the right. This reduces the number of cases we need to handle during restructuring essentially in half. But does it *really*?

Unfortunately this perceived simplicity is at the cost of performance. Despite having fewer cases to deal with when it comes to restructuring, they have to perform those few cases more often, as their are fewer valid asymmetric red/black tree's than there are symmetric. Take as an example the two trees pictured above. Both tree's were built from the same input, but the left leaning variety required 17 right rotations to the red/black tree's 11 right rotations. They don't fare any better for left rotations either, requiring 29 left rotations compared to the red/black tree's 10 left rotations. That's three times the work for a tree that ends up less balanced.

Bottom Up Red/Black Insertion

One often overlooked property of bottom up insertion allows us to simplify our conceptual view of Red/Black trees. If you're one of those people who just couldn't wrap their head around the 2-3-4 tree abstraction from which they derive, you'll be happy to know we that can ignore it entirely utilizing only the red/black framework. Some people find this easier, though I still recommend trying to grok the relationship to 2-3-4 trees. Regardless of which way were looking at it, a valid Red/Black tree must maintain the following properties:

• The root node must be black
• No red node can be the child of another red node
• All paths from the root to the node has the same number of black nodes.
• Every Red/Black Tree must also be a valid binary search tree.

To add a node bottom up in a Red/Black tree, you begin by performing a regular BST insertion at a leaf. All newly inserted nodes in a Red/Black tree are colored red. As usual, null links are considered black. If the newly inserted node also happens to be the root node, we simply color it black, and we're done. In fact, we end every insertion by setting the root's color to black. Why? Because part of balancing in red black tree's involves "pushing" red nodes up the tree during color flips. If during balancing, the red node makes it to the root, we can then "push" it up out of the tree, restoring black balance.

node* putRB(node* x, K key, V value) {
      if (x == nullptr) {
           count++;
           return new node(key, value);
      }
      if (key < x->key) x->left = putRB(x->left, key, value);
      else x->right = putRB(x->right, key, value);
      return fixInsert(x);
}
void insert(K key, V value) {
      root = putRB(root, key, value);
      root->color = black;
} 

Inside fix insert we're going to use the same isRed() and colorFlip() methods as for left leaning red black trees. For rotateLeft() and rotateRight() I've used the same methods as in my other various implementations of red black tree's and AVL trees. This separates the logic of node coloring from rotations. No mixing of concerns!

bool isRed(node* x) { 
     return (x == nullptr) ? false:(x->color == red); 
}
node* colorFlip(node* x) {
      x->color = !x->color;
      x->left->color = !x->left->color;
      x->right->color = !x->right->color;
      return x;
}
void swapColors(node* x, node* y) {
      bool tmp = x->color;
      x->color = y->color;
      y->color = tmp;
}
node* rotateRight(node* x) {
      node* y = x->left;
      x->left = y->right;
      y->right = x;
      return y;
}
node* rotLeft(node* x) {
      node* y = x->right;
      x->right = y->left;
      y->left = x;
      return y;
} 

If one so desired, they could replace all calls to swapColors() by adding the following to both rotateLeft() and rotateRight(). The direct comparison with Left Leaning Red/Black trees below used this method.

y->color = x->color;
x->color = red;

All of the tri-node restructuring takes place in the fixInsert() method. The decision of when to rotate is determined by the color of the newly inserted nodes uncle, in combination with the orientation of the node with respect to it's parent and grandparent. If a newly inserted nodes parent and it's sibling are both red, we can perform a colorFlip() on the nodes grandparent, balancing the tree without requiring any rotations. Otherwise we have two symmetrical cases to handle for when the nodes uncle is red. We have to address these cases in the event the the current nodes left child is red and right child is black, as well as for the inverse case when the nodes right child is red and left child is black:

node* fixInsert(node* x) {
     if (isRed(x->right) && isRed(x->left)) 
           x = colorFlip(x);
     if (isRed(x->left)) {
          x = handleLeftIsRed(x);
     }
     if (isRed(x->right)) {
          x = handleRightIsRed(x);
     }
     return x;
} 

The code for handleLeftIsRed() and handleRightIsRed() are mirror images of each other. They each address two conditions. The first condition is that both the node and its parent are aligned. This can be balanced by swapping the parent's color with its grandparent, and doing a single rotation on the grandparent. The other case is when the node and its parent are not aligned and requires a double rotation to bring the tree back in to balance.

node* handleLeftIsRed(node* x) {
       if (isRed(x->left->left)) {
            swapColors(x, x->left);
            x = rotateRight(x);                
       }                               
       else if (isRed(x->left->right)) {
           x->left = rotateLeft(x->left);
           swapColors(x, x->left);  
           x = rotateRight(x);            
      }
      return x;
}
node* handleRightIsRed(node* x) {
      if (isRed(x->right->right)) {
          swapColors(x, x->right);
          x = rotateLeft(x);
      } else if (isRed(x->right->left)) {
         x->right = rotateRight(x->right);
         swapColors(x, x->right);
         x = rotateLeft(x);
     }
     return x;
} 

And that's all there is to it. I had formatted the code in a way to make it as understandable as possible, but the balancing code can be written inline with the insert operation as is done with Left Leaning Red Black Tree's in "Algorithms"(4th ed).

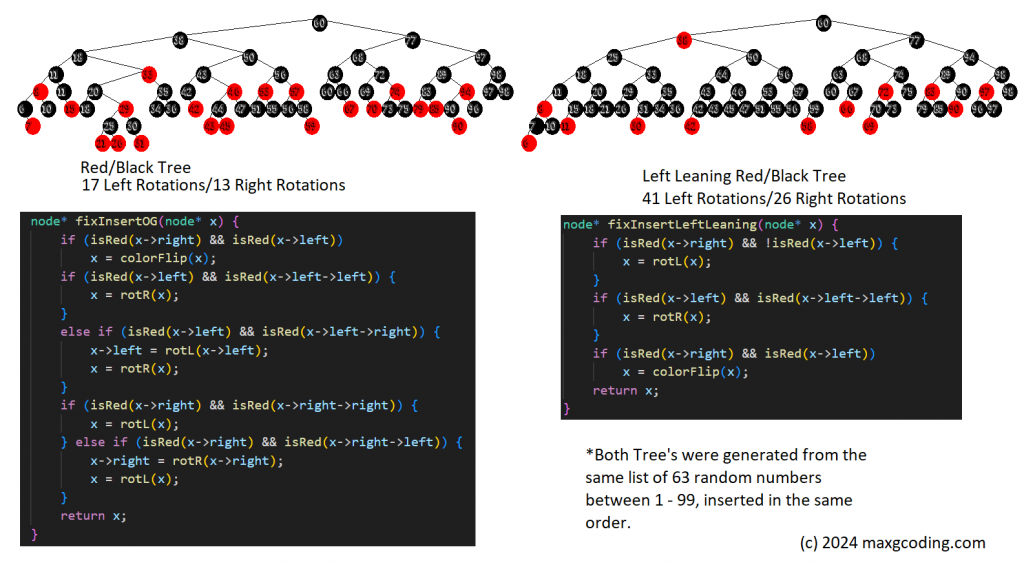
When you comparing the two algorithms side by side, the idea that the left leaning variety is any magnitude simpler evaporates. Don't get me wrong: I have nothing but the utmost respect for Dr. Sedgewick, and one can argue that being a professor of computer science, his primary concern is the presentation of material in a way that is agreeable to his students. However, I believe this can be done without compromising the integrity of the algorithms being presented. Further, I believe it is actually to the detriment of future computer science students to advocate for the learning of conceptually simpler but less efficient algorithms, especially when "conceptually simpler" equates to the removal of two If statements in practice.

Until next time, happy hacking!

 

---